Square Within a Square

Nicole Mosteller

EMAT 6690

Prove that quadrilateral WXYZ is a square.

Figure 1.

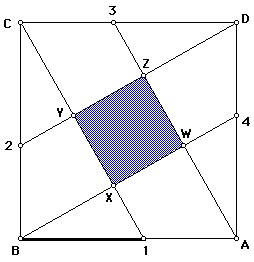
Since ABCD is given to be a square, we have many properties of ABCD that can be used to arrive that WXYZ is a square. First remember, that the opposite sides of ABCD are parallel, consecutive sides of ABCD are perpendicular, and all sides of ABCD are congruent. These properties will be used to show that for WXYZ the . . .

1. Opposite Sides are Parallel

2. Consecutive Sides are Perpendicular

3. All Sides are Congruent

Figure 2.

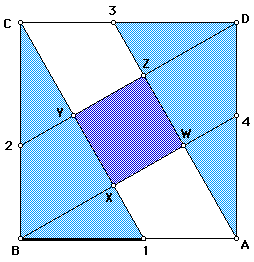
First note that the highlighted triangles are congruent (SAS). Likewise, two more triangles drawn within square ABCD are congruent (take the highlighted triangles and rotate 90 degrees). It is the corresponding parts of these triangles that we will be investigating in Figure 3 (below).

Figure 3.

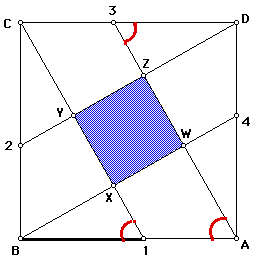
The angles marked with vertices at 1 and 3 are congruent (CPCTC). Because AB//CD, we know that the marked angles at points A and 3 are congruent (alternate interior angles). Using the transitive property, we know that the marked angles at 1 and A are congruent. These are corresponding angles created by the transversal AB which makes the sides YX//WZ.

This same argument can be made to show that ZY//WX.

Figure 4.

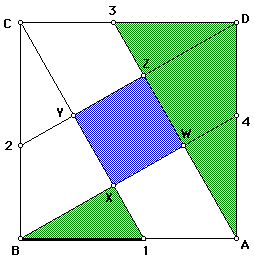
The marked corresponding angles from Figure 3 leads directly the second part of our proof. We know that two of the corresponding angles in the highlighted triangles are congruent (i.e. the angle with vertex B is congruent to the angle with vertex A, and the angle with vertex 1 is congruent to the angle with vertex 2). Since these highlighted triangles are similar (AA), the third corresponding angles are congruent as well. The angle with the vertex at X is congruent to the angle with the vertex at D. Since the angle at D is created by two perpendicular lines, and the angle at X must have the same measure as the angle at D, so XW is perpendicular to XY.

This same argument can be made to show that the other consecutive sides are perpendicular as well.

Figure 5.

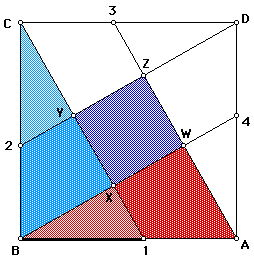
To show that all of the sides WXYZ are congruent, let's start with the highlighted triangles in Figure 5. Triangle ABW is congruent to Triangle BCX (ASA). This means that BW is congruent to CX (CPCTC). Next, the smaller highlighted triangles are also congruent (ASA). This means that BX is congruent to CY (CPCTC). Using the subtraction property, BW - BX = CX - CY, we see that XW is congruent to YX.

This same argument can be made to show that all sides are congruent.

Figure 6.

WXYZ is a square because

1. Opposite Sides are Parallel (See Figure 3);

2. Consecutive Sides are Perpendicular (See Figure 4);

3. All Sides are Congruent (See Figure 6).

 

RETURN TO INTRO | Continue Investigaiton