The probability of an event is a number describing the chance that the event will happen. An event that is certain to happen has a probability of 1. An event that cannot possibly happen has a probability of zero. If there is a chance that an event will happen, then its probability is between zero and 1.

Examples of Events:

• tossing a coin and it landing on heads
• tossing a coin and it landing on tails
• rolling a '3' on a die
• rolling a number > 4 on a die
• it rains two days in a row
• drawing a card from the suit of clubs
• guessing a certain number between 000 and 999 (lottery)

Events that are certain:

• If it is Thursday, the probability that tomorrow is Friday is certain, therefore the probability is 1.
• If you are sixteen, the probability of you turning seventeen on your next birthday is 1. This is a certain event.

Events that are uncertain:

• The probability that tomorrow is Friday if today is Monday is 0.
• The probability that you will be seventeen on your next birthday, if you were just born is 0.

Let's take a closer look at tossing the coin. When you toss a coin, there are two possible outcomes, "heads" or "tails."

Examples of outcomes:

• When rolling a die for a board game, the outcomes possible are 1,2,3,4,5, and 6.
• The outcomes when choosing the days of a week are Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, and Saturday.
• When selecting a door to be chosen behind on the game show "Let's Make a Deal," the outcome of the choices is door 1, door 2, and door 3.

• A die is rolled and the number on the top face is recorded. All the integers from 1 to 6 are possible. So S = {1, 2, 3, 4, 5, 6}.
• A pair of dice are rolled and the sum of the numbers on the top faces is recorded. The smallest sum is 1 + 1 = 2; the largest is 6 + 6 = 12; and all the integers in-between are possible. So S = {2, 3, 4, ..., 11, 12}.

The two outcomes of tossing a coin are equally likely, which means that each has the same chance of happening. When all outcomes of an event are equally likely, the probability that the event will happen is given by the ration below.

When looking at the probability of the event that the coin lands on tail we get the following:

These events are equally likely to happen:

• When there is a 50% chance of rain, that means that there a chance that it might rain, but that there is also a chance that it might not rain. These chances are the same so the event is equally likely to happen.
• When one rolls a game die, he/she has exactly the same chance of landing on any of the six sides. Therefore the probability of landing on any one specific side would be 1/6. This is also true for any spinner. Say a spinner is divided into 10 sections. Then there is an equally likely chance that the spinner can land on any of the sections. Thus the probability for the spinner to land in any designated section is 1/10.
• The probability of selecting one of the three doors on the game show is also equally likely. There is no bias over the contestants decision so each door has a probability of 1/3 being chosen. This is true if there are no arrows pointing towards one of the doors.

When the outcome of one event does not affect the outcome of a second event, the events are independent. When the outcome of one event does affect the outcome of the second event, the events are dependent. Let's look at the following five examples. Decide which pair of events are dependent or independent.

1. Toss a coin. Then roll a number cube (die).

2. Choose a bracelet and put it on. Choose another bracelet.

3. Select a card. Do not replace it. Then select another card.

4. Select a card. Replace it. Select another card.

5. Pick one flower from a garden, then pick another.

The events above that are independent are numbers 1 and 4.

Probability of Two Independent Events

Given a coin and a die, what is the probability of tossing a head and rolling a 5?

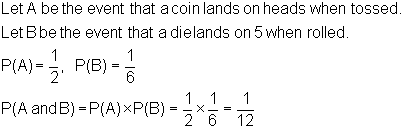
The events above that are dependent events are numbers 2, 3, and 5.

Probability of Two Dependent Events

Given a deck of cards, what is the probability that the second card drawn will be from the same suit if the first card drawn is the Queen of Hearts?

The number of outcomes of an event is the product of the number of outcomes for each stage of the event.

Let's suppose that we want to find out how many different license plates are possible, when the license plate is composed of three digits then three letters. To do this you can use the counting principle. The product below gives the number of different plates possible.

We can use this same principle even if there are stipulations on the problem. For example say that a number or letter can only be used once.

What if we wanted to know which plate system provided more possible outcomes, one with five letters or one with seven digits?

Five letters:

Seven digits:

So we see by using the counting principle that there are more possibilities if we use five letters instead of seven digits.

Statistics for Middle School

RETURN TO OUR HOME PAGES

Cathy Brooks Laura Dickerson