

Go to Assignment 7 for explanation of information/problem/write-up.
Problems:
1. Make a script for construction of the tangent circles.
2. Construct the tangent circle to two given circles if the given point is on the smaller of the two circles
a. so that the smaller circle is external to the tangent circle.
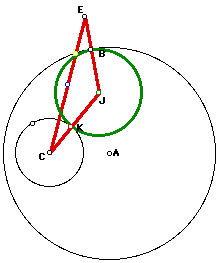
b. so that the smaller circle is internal to the tangent circle.
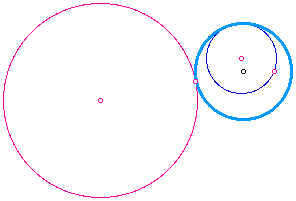
These constructions took so long to figure out. I do not think my middle schoolers would even bother with this unless I forced them to do it...or threatened them...whichever came first...
To say the least, I did not enjoy this construction because it gave me a huge headache!!!
On a lighter note, if you look at my constructions in both a and b, you will notice some similarities. I used the same script for both, yet in construction b, I had to move points around (actually, all I did was to move my point of tangency around the big circle or around its circumference) in order to get my beautiful picture.
Take a look at my script so you can experience the feel of tangent circles...make sure to create four points first so the creations may continue!
4. Discuss the loci of the centers of the tangent circles for both 1a and 1b.
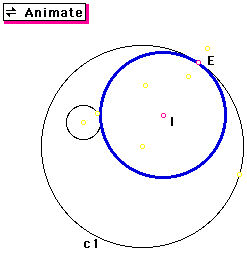
After recreating my construction
of the tangent circle for the sixth time, I finally got it right!!!
The script that I guided you to look at before, may or may not
be correct...why don't you find out the differences between the
following:
Did you notice that the locus of the tangent circles is an ellipse?
What happens when you change the position of the tangent circle? Does the ellipse stay the same? Does the ellipse become something else? Why not doodle with the Geometer's Sketch Pad to see what will actually happen? Again, make sure that you select four points. Do not go below the link as the picture will reveal my answer.
Answer: Because the tangent circle overlaps the original circle, the trace becomes a hyperbola.
Extra Credit: What is the difference between a parabola and a hyperbola?

Investigate. . . what else can you find?
Write-up: This investigation was quite hard for me to understand, simply because I had never had any hands-on work with locus or tangent circles. It took me quite a long time to even come to the last picture (above).
I certainly do not want my students to go through as much anguish as I did with this problem. Although...I must say, some anguish is good for the true problem solver, especially if he/she is not afraid to ask for help or to search other realms of the world.