Area Pedagogical Extension
by: Kelli Nipper

Does Pick's Theorem work for other figures?

Objective: Picky Nicky will investigate various shapes by considering the number of boundary and interior points.

Materials: dot paper and/or Geoboard and/or Geometer's Skechpad.

Assignment:
1. Construct the following figures:
a) a triangle with no interior points and 4 boundary points
b) a quadrilateral with 1 interior point and 8 boundary points
c) a square with 4 interior points (How many boundary points?)
d) any figure with 5 interior points and 10 boundary points.

2. Find the area of each of the following:

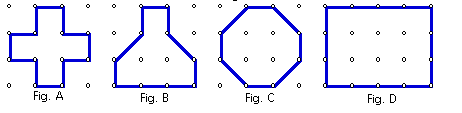
a)____________ b)____________ c)____________ d)____________

3. In the chart, record the number of boundary points(B), Interior Points(I) and Area for Fig. A,B,C,D.

4. Do these areas hold true for Pick's Theorem: Area = (B - 2 + I)/2

5. On the basis of the patterns you have discovered, what conjecture would you make for the area of any figure with B boundary points and I interior points?

Return to Pick's Theorem