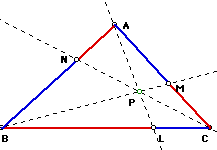
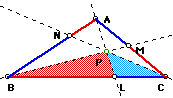
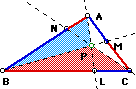
 any
triangle ABC (diagramed below), select a point P inside the triangle
and draw lines AP through to L, BP through to M, and CP through
to N. Explore the ratio:
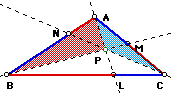
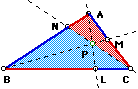
any
triangle ABC (diagramed below), select a point P inside the triangle
and draw lines AP through to L, BP through to M, and CP through
to N. Explore the ratio:PART I - INVESTIGATION #1
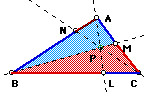
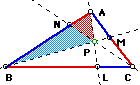
Given  any
triangle ABC (diagramed below), select a point P inside the triangle
and draw lines AP through to L, BP through to M, and CP through
to N. Explore the ratio:
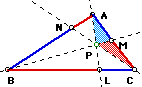
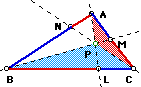
any
triangle ABC (diagramed below), select a point P inside the triangle
and draw lines AP through to L, BP through to M, and CP through
to N. Explore the ratio:
PROOF OF ABOVE CONJECTURE:
To prove the above conjecture I will use some key ideas about area and similarity of triangles. I one key idea that I want to introduce now so that I can use it freely later without much explanation is:
Equivalent Ratios of Area and Sides of a Triangle
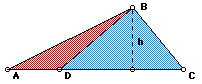
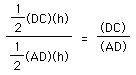 The ratio of
the two pieces of AC is equal to the ratio of the two areas formed
on those two pieces.
The ratio of
the two pieces of AC is equal to the ratio of the two areas formed
on those two pieces.
For easy reference I will refer to this fact as ERAST.
|
|
||
 |
|
|
 |
|
|
 |
|
|
|
|
||
 |
 |
 |
|
|
||
 |
 |
 |
|
|
|
|
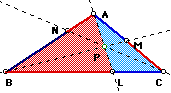
Using the final summary of each stage we see the proof come to a close:
Finally 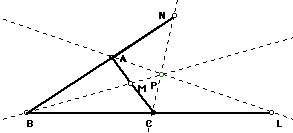 I
will say that when the point P is outside the triangle two of
the area relationships become negative while the other one remains
positive. Thus when the three ratios are multiplied together we
still get a positive 1 value. I will leave the proof of this up
to the reader.
I
will say that when the point P is outside the triangle two of
the area relationships become negative while the other one remains
positive. Thus when the three ratios are multiplied together we
still get a positive 1 value. I will leave the proof of this up
to the reader.
PART I - INVESTIGATION #2
PROBLEM: Given a rectangular sheet of cardboard 15 inches by 25 inches. If a small square of the same size is cut from each corner and each side folded up along the cuts to form a lidless box. What is the maximum volume of the box? What size(s) of the square would produce a box of volume equal to 400 cubic inches?
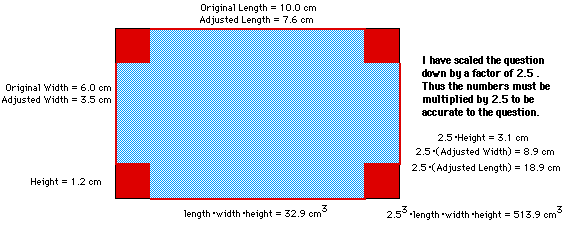
Approach #1 - Using Geometer's Sketchpad I created a scaled down version (by a factor of 2.5 and in cms) of the question to see its visual representation. Using this method I found the maximum volume to be approximately 514 cubic inches. (See the sketch)
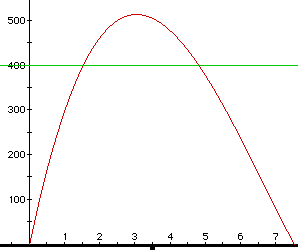
Approach #2 - Using Algebra expresser to graph the relationship y = x(25 - 2x)(15 -2x). The resulting graph was found:
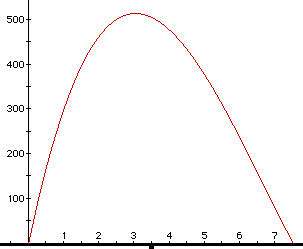
This seems to verify that the maximum volume is close to 514 cubic cms.
Approach #3 Using a spreadsheet we can approximate the answer even closer. Using Claris works I found the maximum volume to be:
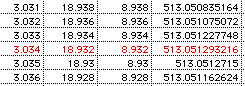
Using the precision of a spreadsheet I was able to find that the maximum volume is 513.05129 cubic inches. This of course is still an approximation, but one much closer then the previous two approaches. This also tells us that the side of the square piece to cut out is 3.034 inches.
Concerning the second question: What size(s) of the square would produce a box of volume equal to 400 cubic inches? We represent this two ways quite easily from the work we have already done.
Approach #1 - Algebra Xpresser shows us that there are two possible values such that a volume of four hundred occurs. Using a guesstimate I would say at 1.5 and 5.
Approach #2 Using a spreadsheet I hope to find a more precise way of determining the values.

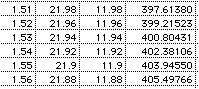
At approximate values of 1.525 and 4.795 we see the volume of the lidless box be 400 cubic inches. All of these methods are simply devises to approximate the value. The spreadsheet seem to be the best of the above methods in terms of precision while the others gave a good visual representation.