The students ability to examine the shape, and characteristics of graphs has increased dramatically with the use of technology in the classroom. In the past, much of their time was spent on the painstaking process of generating numerous points in hopes to find the shape of the graph. Even this method did not always clearly define what was going on between the chosen points. The technology performs the process of graphing for the student quickly, leaving the student time to interpret and analyze. I do wish to say that I am not advocating that students don't need the skill of graphing, I am simply stating that use of technology can increase a students ability to understand the patterns to graphing. In this paper I wish to look at two models for examining quadratic roots using technology, one being the standard practice and the other being a little less orthodox.
PROCESS: It has now become rather standard exercise, with available technology, to examine a quadratic equation by the process of overlaying several graphs. A student might be instructed to manipulate the different values of a, b, and c while holding the other two variables constant. From these graphs discussion of the patterns for the roots can be followed. For example, if we set the coefficient of the linear term bx to b = -3, -2, -1, 0, 1, 2, 3, and overlay the graphs, the following picture is obtained.
 |
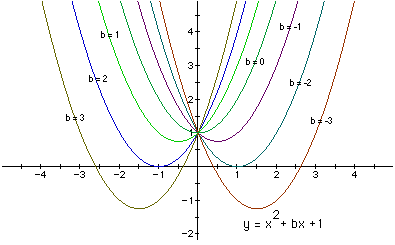INTERPRETATION: This process reveals quite a bit of information about the quadratic equation that we are studying. We can discuss the "movement" of a parabola as b is changed. The parabola always passes through the same point on the y-axis ((0,1) with this equation). For b > -2 or b < 2 the parabola intersects with the x-axis into two locations giving two real roots. When b = 2 or when b = -2 the parabola is tangent to the x-axis and so the original equation has one real root at the point of tangency. Finally when -2 < b < 2, the parabola does not intersect the x-axis - thus the original equation has not real roots.
PROCESS: Let us now approach
the same discoveries in a different way. Since we are looking at the quadratic
equation in terms of its roots we can simplify the equation to:.
Notice how y is a fixed value of zero, leaving us with
the two variables x and b. Instead of using the familiar technique of graphing
in the xy plane, we will use the xb plane.
 |
 |
 |
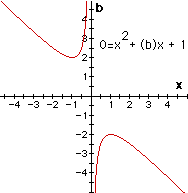INTERPRETATION: It may take a moment to see what this represents. The graph on the left shows all the values for b such that real roots exist. The graph on the right shows how we could quickly estimate the roots of the equation. For example, when b = 3 (as shown above) the two roots of the equation are approximately x = - 0.4 and x = - 2.6. The xb plane not only gives us a quick reference to the all the values of the roots for some b but we can also examine what type of roots, and whether they will be positive or negative.
 |
 | |
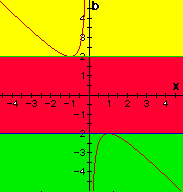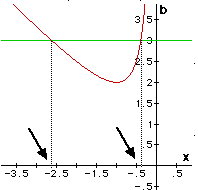
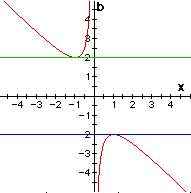
(Green) b = 2 one negative real root (Blue) b = - 2 one positive real root A point of tangency, thus one root. |
(Yellow) b > 2 two real negative roots. (Green) b < - 2 two real positive roots. (Red) - 2 < b < 2 no real roots | |
Thus using one equation in the "xb" plane we were able to deduce all the information that several graphs produced using the "standard" method.
PROCESS: Using a similar approach
as the "xb" plane, we will look at the "xc" plane. The
equation simplifies to: 
Notice how y is a
fixed value of zero and b = 4, leaving us with the two variables x and c.
Let us determine all the values for c that produce roots.
 |
 |
 |
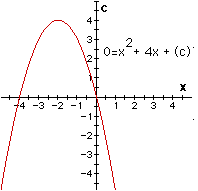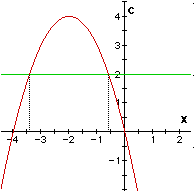INTERPRETATION: The graph on the left shows all the values for c such that real roots exist. The graph on the right shows how we could quickly estimate the roots of the equation. For example, when c = 2 (as shown above) the two roots of the equation are approximately x = - 0.6 and x = - 3.4. The xc plane not only gives us a quick reference to the all the values of the roots for some c but we can also examine what type of roots, and whether they will be positive or negative.
 |
 | |
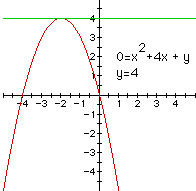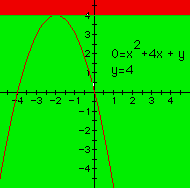(Green) c = 4 one negative real root A point of tangency, thus one root. |
(Red) c > 4 no real roots. (Green) 0 < c < 4 two negative real roots. (Green) c < 0 two positive real roots. | |
 |
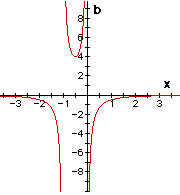What does this graph represent?
What does it mean if I wanted to know the roots when b = 6 or when b = - 6?
|