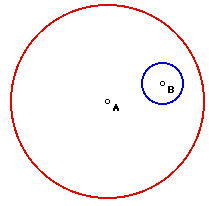
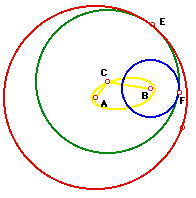
Given two circles, the red circle with center A and the blue circle with center B, we want to create a circle that is tangent both. The diagram on the right shows one possible way of constructing that circle, this is referred to as the interior tangent circle.

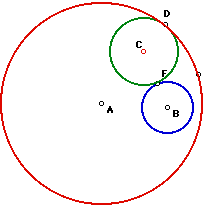How the tangent circle is constructed becomes very important in terms of the interpretation of the locus of the points created by tracing its center. CONSTRUCTION: Given two fixed circles (red & blue) create a circle that is tangent to both circles. B is the center of the blue circle and E is the intersection of the extended diameter of circle A (red) with the circle D. Two important points is that circle D has the same radius as circle B (blue) and that we use the external intersection point E. 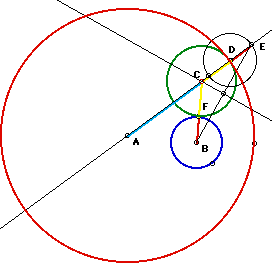The perpendicular bisector of BE intersects the diameter at C, which forms an isosceles triangle. The equal arms of the isosceles triangle (CE & CB) minus BF & DE respectively results in two equal length segmennts from C that touch the red circle and the blue circle once. This point C is the center of the new green tangent circle.

Some key measures:

BF = DE = radius of fixed blue circle

AC + CD = AD = radius of fixed red circle

AC + CF = AD = radius of fixed red circle

(AC + CD) + DE = fixed red radius + fixed blue radius

(AC + CF) + BF = fixed red radius + fixed blue radius

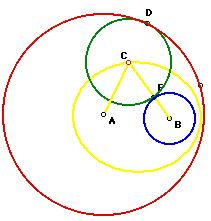Now when we trace the path of point C,the center of the tangent circle, point C, we find that an ellipse appears. An ellipse in general is created when the sum of the distances between two focal points is fixed. In this case the focal points are point A, the center of the red circle, and the point B, the center of the blue circle. We can now turn to the construction of the green tangent circle to find the fixed values.

As stated above

AC + CF + BF = fixed red radius + fixed blue radius

The two radii are unchanging for all possible tangent circles, thus an ellipse is formed.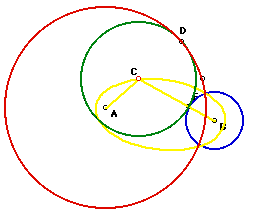

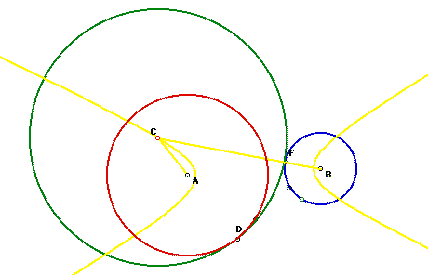
If the two orignal circles were overlapped a similar situation occurs. An ellipse is formed. This is an interesting process to watch as the green tangent circle exit and enter the red circle to create the locus of points inside the blue circle.

The distance from A to C to B is exactly the addition of the two radius's of the blue and red circles. If the blue circle was pulled completely separate from the red circle it would create a fixed difference between the centers instead of a fixed sum . The shape created by a fixed difference between two points is called a hyperbola.

By the nature of the construction of the tangent circle, the center of the circle will produce the locus of points that have a fixed difference. That difference will be the the addition of the two fixed radius's of the red and blue circle.

CLICK HERE TO TRY IT OUT !!

If this didn't work, click here.

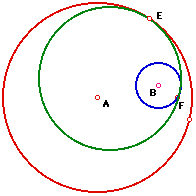
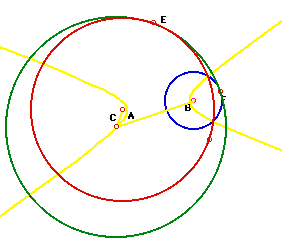
Given two circles, the red circle with center A and the blue circle with center B, we want to create a circle that is tangent both. The diagram on the right shows one possible way of constructing that circle, this is referred to as the exterior tangent circle.

CONSTRUCTION: Given two fixed circles (red & blue) create a circle that is tangent to both circles. 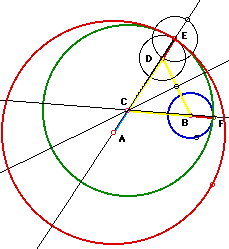B is the center of the blue circle and D is the intersection of the diameter with the circle E (internal intersection) Circle E has the same radius as blue circle B. The perpendicular bisector of BD intersects the radius at a point C . Point C is equal distance from point E and point F. Thus point C is the center of the new green tangent circle.

Some key measures:

BF = DE = radius of fixed blue circle

AC + CD + DE = AE = radius of fixed red circle

AC + CB + BF = AE = radius of fixed red circle

AE - DE = fixed red radius - fixed blue radius

(AC + CF) - BF = fixed red radius - fixed blue radius

Now when we trace the locus of points that are created by the center of the green tangent circle, point C, we find that an ellipse appears. The fixed value is created by the unchanging radii of the two given (red & blue) circles.

As stated above

AC + CB = AE - BF = fixed red radius - fixed blue radius

.

If the two orignal circle overlap a hperbola is formed. This occurs the point of tangency on the blue circle is extended beyond the fixed distance.

When the two original circles (blue & red) are disjoint, the pattern of the hyperbola will continue because at any stage where any given point of the blue circle is extended outside the red circle a hyperbola will be formed.

CLICK HERE TO TRY IT OUT !!