

Let triangle ABC be any triangle. Then if P is any point in the plane, then the triangle formed by constructing perpendiculars to the sides of ABC (extended if necessary) locate three points R, S, and T that are the intersections. Triangle RST is the Pedal Triangle for Pedal Point P. This definition is illustrated in Figure 1.
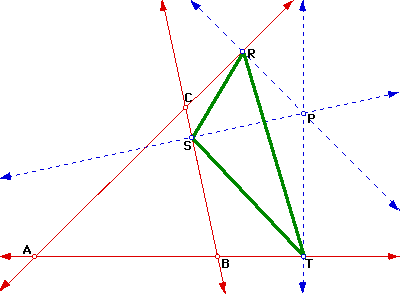
Now let us investigate the pedal triangle when pedal point P is located in the following positions:
1. What if pedal point P is the Orthocenter of triangle ABC ? Even if outside ABC?
2. What if . . . P is the Circumcenter . . . ? Even if outside ABC?
3. What if P is one of the Vertices of triangle ABC?
If you have not looked number three above, it is worth looking at because the following discussion will be an extension of that pedal point position and its pedal triangle.
As was seen in number three above, the pedal triangle becomes a degenerate triangle and forms the Simson line when the pedal point is located at one of the vertices of triangle ABC. Is there any other points where the pedal triangle becomes degenerate and a the Simson line is formed besides when located at one of the vertices of triangle ABC? One may want to try looking at the pedal triangle when the pedal point is on the circumcircle since the circumcircle passes through each vertice of triangle ABC. This is illustrated in Figure 1 below.
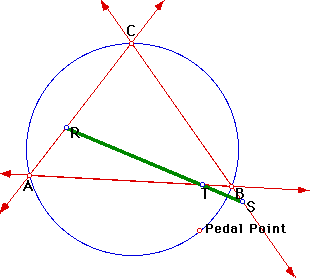
From this image you can see that when the pedal point is located on the circumcircle, the Simson line is formed. If you think that the location of the pedal point in Figure 1 is just another special case of when the Simson line occurs and you are not yet convinced that a pedal point on the circumcircle always creates a Simson line, go to GSP for an animation of the pedal point on the circumcircle to see for yourself.
Continuing with this discussion on Simson lines. Is there a point on the circumcircle for the pedal point that makes the Simson line one of the sides of the triangle ABC? As can be seen in Figure 2, there is indeed such a point, and by moving the pedal point around one can find the location where the Simson line is the same segment as as the other two sides of triangle ABC as well.
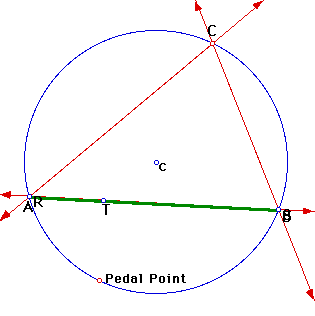
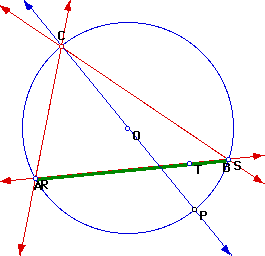
Now that it has been found that the Simson line can lie along a side of triangle ABC, is there any way to predict where the pedal point needs to be located in order for this to occur? By looking at Figure 2, one can notice that the pedal point, c(the center of the circumcircle) and vertice C seem to lie on a common line. After constructing the line through points c and C, it becomes clear that when the pedal point is located on this line the Simson line becomes one of the sides of triangle ABC. Figure 3 illustrates this point.
In closing this discussion on pedal points and triangles, we will look at a few other interesting items that they create. If one was to trace the midpoints of the sides of the pedal triangle, what would you think the resulting shapes would look like? Circles? Lines? Parabolas? Ellipses? By looking at Figure 4, you can see that the midpoints of the pedal triangle trace out the paths of ellipses.
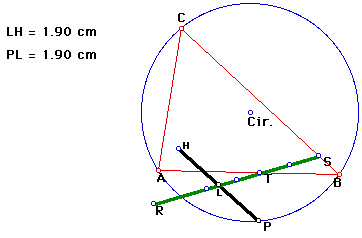
Another interesting consequence that occurs, comes from the intersection between the Simson line and the line segment connecting the pedal point P and the orthocenter H of triangle ABC. The point where these two line segments intersect turns out to be the midpoint of the line segment through P and H. Figure 5 displays this occurrence.
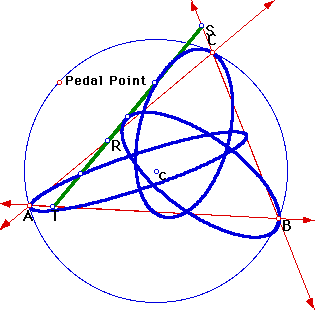
If one was to trace the lines that formed the segments that make up the sides of the pedal triangle while the pedal point was moving around the circumcircle, what would one expect to see? When tracing lines, envelopes generally form defining some type of shape. What shape would you expect to form from tracing P around the circumcircle, to make the previous question a little more direct? As may have been expected, the lines forming the pedal triangle when traced form an envelope that resembles a triangle, as can be seen in Figure 6.

This concludes all of the discussions about pedal points and triangles. However, there are many other interesting items to investigate that are not presented here. If the reader feels so inclined to investigate further, some possible investigations may include: