

Consider any triangle ABC. Select a point P inside the triangle and draw the lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively. Explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles and various locations of P.
Conjecture? Prove it! Also, consider the ratio (AF)(BD)(EC)/(FB)(DC)(EA).
This investigation discusses the relationship between similar triangles. We begin with triangle ABC and a point P arbitrarily placed inside the triangle.
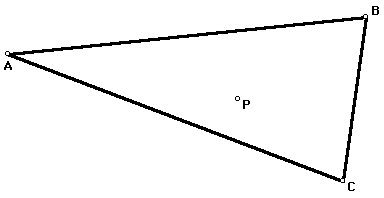
To produce the relationships and the similar triangles, we connect point P with each vertex of the triangle.
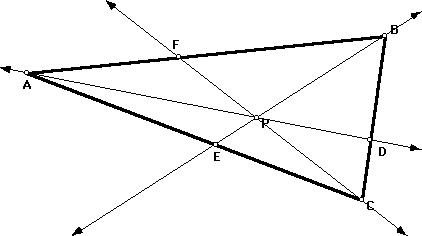
Our goal is to prove that (AF)(BD)(EC) and (FB)(DC)(EA) are equal. One approach is to prove that the ratios are equal to one.
The following image shows the lengths of the sides that are to be multiplied together. I have also created some parallel lines to help us locate and recognize the similar triangles.
The lines are parallel to AD, which passes through point P.
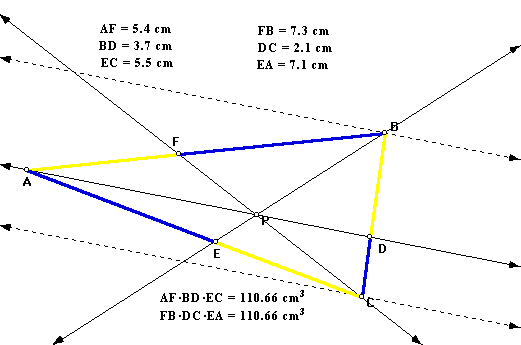
To prove that (AF)(BD)(EC) and (FB)(DC)(EA) are equal it is suggested to show that their ratios are equal to one.
That is
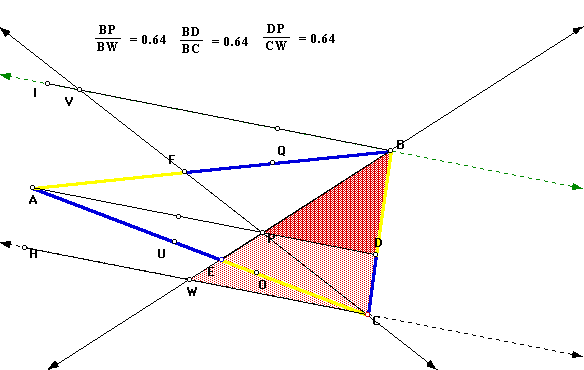
Our first set of similar triangles can be found using the lines parallel to PD and sharing the angle B. Because the two triangles share the angle B and have parallel bases, we know that the sides will be in proportion and therefore the triangles will be similar.
Therefore
The next set of similar triangles follow along the same thought pattern. You can prove their similarity using PD and VB, which are parallel. The triangle CBV and CDP share the angle C and have parallel bases. The parallel bases create two pairs of sides that are proportional. With these characteristics we can say that the triangles are similar.
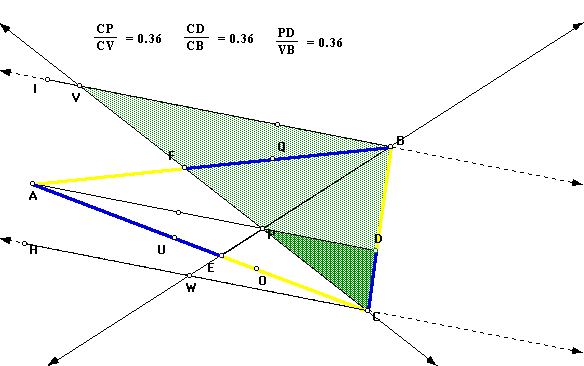
Therefore
Again, the parallelity of lines help to prove the similarity of the next sets of triangles. We can prove that triangle CPW is similar to triangle BPV through the Angle-Angle theorem of similarity. In the image below it is easy to see the vertical angles BPV and CPW created by the intersection of BW and CV. Vertical angles are equal. The next pair of equal angles are created by parallel lines (the extensions of CH and BI) and the transversals BW and CV, respectively.
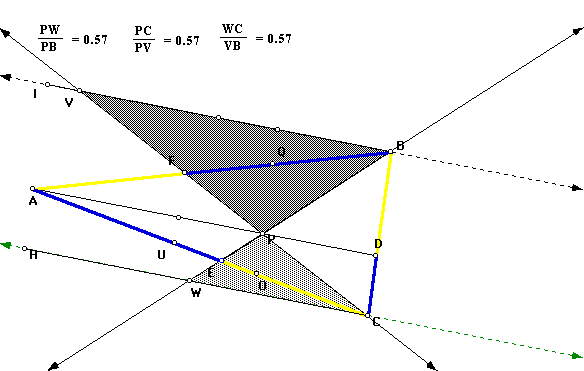
Therefore
Again, we turn our attention to triangles that have parallel bases and any angles that may have the same measurement. The parallel lines cut by transversals help to create angles that are equal, thus allowing the Angle-angle theorem of similarity to hold once again. The images below were found to be similar using this approach.
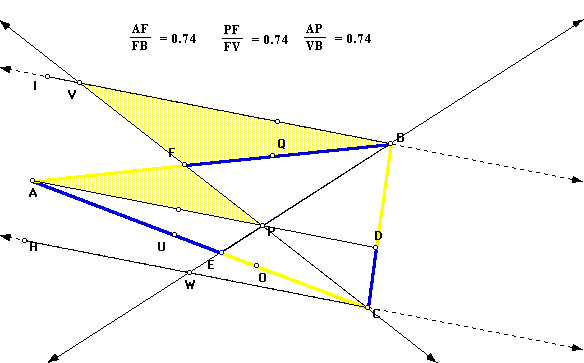
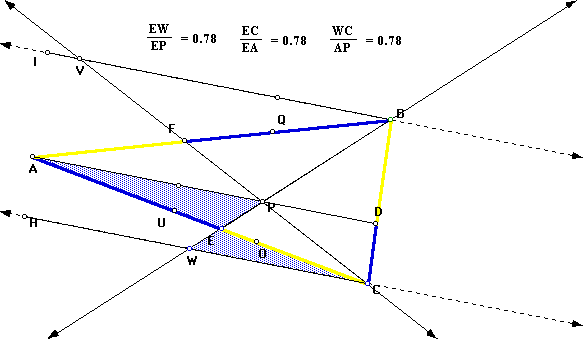
Therefore
Now that we have determined the relationships between all of the similar triangles in our figure, we need to bring it together and prove our original ratio
We need to manipulate the ratios that we know are equal to create a ratio that is demonstrably equal to one. To enable us to reach our goal, we should substitute some known values.
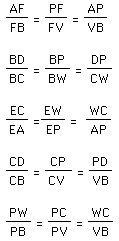
We can substitute
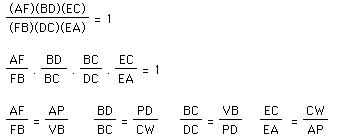
Because
we can use the transitive property of multiplication and conclude that