Angle of View

Click here for a problem description

The objective is to maximize the angleABC in the sketch below, where B represents the point from which you are viewing the the billboard AC.

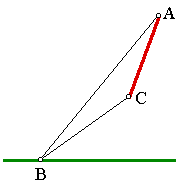
Consider the circumcircle of triangle ABC. This circle will meet the green line in at most two places.
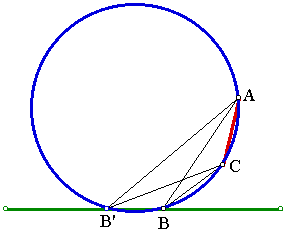
Click for a Circumcircle script.
The angle ABC will be a maximum when the circle containing A, C and B is tangent to the green line. The task then is to construct a circle given A and C and the green line. This construction is dealt with in Apollonius problem.
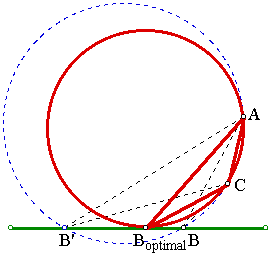
Click here for the GSP script

How can we determine the optimal position of B directly? This follows directly from the following geometric statement:

Given a circle with tangent t meeting the circle at B and with secant s meeting the circle at A and C. Let t and s meet at I then:

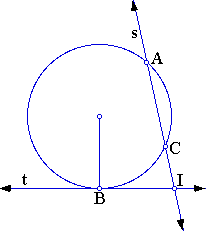
This fact is also the principle underlying the construction used earlier.

Return