

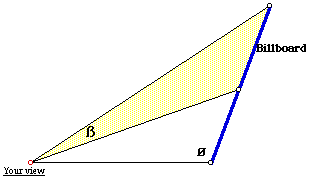
You are standing on level ground in front of a billboard. When you look up at it, the top of the billboard measures a feet up the support from eye level and the bottom of the billboard measures b feet up the support from eye level. You wish to position yourself in order to maximize your "viewing angle" (the angle between the lines of sight of the top and the bottom of the billboard). However, a storm has tilted the billboard, as shown in the accompanying figure. Find the distance x that maximizes ß.
For comments and solution suggestions, click here.
For a GSP file to animate, Click Here.
References:
Problem 532, Computers and Mathematics Education. Proposed by Mike Chamberlain and Mark D. Meyerson, United States Naval Academy, Annapolis, MD
Note: This problem was discussed in Polya, G., (1954) Mathematics and plausible reasoning. Volume 1, Induction and analogy in mathematics. Princeton, NJ: Princeton University Press, pp. 122-125.In the History of Mathematics, this problem is sometimes discussed as the Problem of Regiomontanus -- an alias for the astronomer Johann Muller (also known by several other names). The alias come from the Latin Regio Monte, meaning literally "Royal Mountain" and in time was transformed to Regiomontanus. It is a geometry problem with many implications for trigonometry.