

The triangle ABC has and incircle with Incenter I. The incircle is tangent to the sides of the triangle at points D, E, and F.
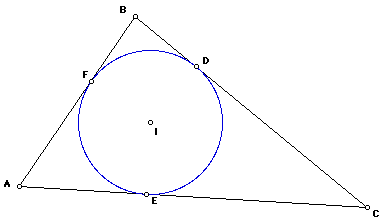
The Gergonne Point is the point of concurrency of the segments AD, BE, and CF.
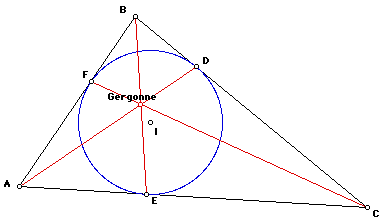
The proof of concurrency is needed. Observe that the Incenter lies on the angle bisectors of the triangle and the radii of the incircle, ID, IE, and IF are perpendicular to the sides. Thus, three pairs of contruent right triangles are formed.
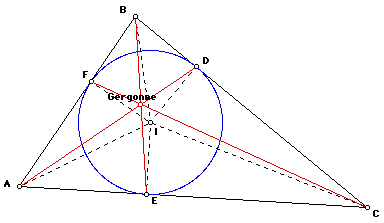
The products (AF)(BD)(CE) and (AE)(CD)(BF) are equal because BF = BD, CD = CE, and AE = AF. Therefore the ratio of the products is 1 and by Ceva's theorem, the three Cevians of the triangle (AD, BE, and CF) are concurrent.