FIGURE 1
The idea of rates that are related to one another in a real world situation applies directly to many problem solving situations. It is therefore a subject for major investigation for a student of the calculus. Related rates here refer to multiple variables in a problem situation, some or all of which are changing with respect to time.
As a first example, let us look at a famous type of calculus related rate problem.
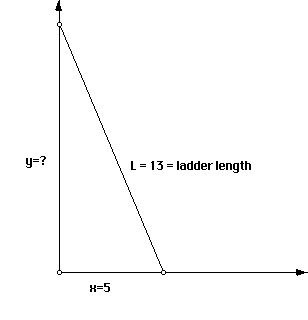
A13 m ladder is leaning against a wall. The ladder slides down the wall at a constant rate of 4 m/sec. How fast is the bottom of the ladder sliding away from the wall when the bottom is 5 meters from the wall?
A picture of course is always desirable. Examine figure 1 below.

FIGURE 1
How can we find the value of y? Of course we can use the Pythagorean theorem, and we find y to be 12. However, the problem we must solve is one of changing quantities (in fact, changing quantities that affect each other, that is, related rates of change). How do we get the rates involved. By now we know that we do so with calculus. Taking derivatives with respect to time will give us the rates we desire. We first, however, must have an equation to represent the situation. Study figure 1 again. Using the Pythagorean theorem, this equation is
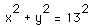 .
.
The big question for the first time calculus student is "Why is the 13 used in place of the variable "L" in this equation, and why isn't the given quantity 5 used in place of "x"? The answer is simple, but the serious student must dwell on it long enough to remember to think about it when setting up equations to solve these type of problems. Any quantity that changes with respect to time as the parameters of the figure change must be represented with a variable. If a quantity is a constant for a particular situation, one may use the given quantity and not a variable. In our situation, "x", the distance of the foot of the ladder from the wall, will change over time (as will "y", the distance from the top of the ladder to the floor); however, the length of the ladder will not change within the context of the given quantities in this given problem situation.
So, how do we determine how fast the bottom of the ladder is moving away from the wall? Looking at figure 1, we see that this is the same as the change in x with respect to time (t). In other words, we want dx/dt. We must however have some equation to represent the problem situation first. We have seen this equation is
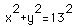 .
.
To get the rates of change involved, take the derivative of this equation implicitly with respect to time. This gives us
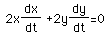 .
.
Solving for dx/dt, we obtain
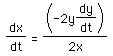 .
.
Now plug in all the given quantities from the stated problem: x=5, dy/dt (the change in y is the ladder sliding down the wall) equals -4 m/s, and y=12m was found using the Pythagorean theorem in fig. 1. Note that the -4m/sec indicates a decreasing y. This gives us
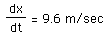 .
.
Here, our answer is positive to indicate an increasing x.
Now let's look at another situation involving related rates.
Suppose we have a square. Inscribed in this square is a circle. See figure 2.
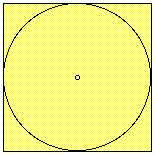
FIGURE 2
The circumference of the circle is increasing at a rate of 1.58 cm/sec. As the circle expands, the square expands to maintain the condition of tangency.
1. How fast is the radius increasing?
2. What is the rate at which the perimeter of the square is increasing?
3. At the instant when the area of the circle is 36pi, how fast is the area "bound by the circle and the square" increasing?
What are the steps to solving this related rate problem? You need a properly labeled sketch. From this you must produce an equation to represent the situation. Then take the derivative with respect to time to get all the related rates involved. Finally, plug in the given information. You may have to solve for certain pieces of information prior to plugging in givens. To see an animation of the sketch, click cir.squ.
Try the problem one question at a time. Then click below for the solutions.
What are some other rates one could find in this problem situation? Ask and solve some problems of your own.
Go back to the sketch cir.squ and try changing the value of dC/dt. What happens to your solutions in the formulas (click "show").? Explain.
Now explore the problem in a spreadsheet environment. Click "another look" to do so.
If you posed the problem with a different set of given information, how would that change the process you used to arrive at an answer? (For example, what if the rate of change of the area of the square had been a given instead of dC/dt? What if the rate of change of the side of the square had been given? What if the rate of change of the perimeter of the square had been given?)
To return to the homepage, click " loondog".