We've already looked at ellipses. Now let's look at inverted ellipses: hyperbolas.
Objectives:
1. Understand what a hyperbola is and how it is constructed.
2. Graph hyperbolas centered at the origin and lying on an axis.
3. Determine the characteristic parts of any hyperbola.
4. Graph any hyperbola regardless of center.
Materials: one sheet of paper and a compass
With the compass, draw a circle on the page. The circle should not take up the entire page. Now, mark a point in the exterior of the circle; that is, mark a point outside of the circle. Fold a point on the circle's boundary to the dot and crease the paper. Continue folding and creasing the paper along the circle's boundary. The hyperbola should eventually appear.
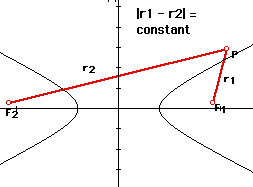
A hyperbola is a set of all points P in a plane such that the absolute value of the difference of the distances from two fixed points is a constant. The two fixed points, F1 and F2, are called foci. The line segments, r1 and r2, from P to the foci are called focal radii at P. The midpoint of the segment F1F2 is the center of the hyperbola.

Open the sketch you made in the Two-Pins-and-a-String Construction (ellipse section). If you do not done the construction or no longer have it, click here for instructions. As you should recall, the circle with center at F1 has a radius of length AC and the circle with center at F2 has a radius of length CB. When you drag point C, the two intersection points of the circles trace an ellipse. Alter the sketch so that it draw a hyperbola.
Q1. Experiment with different locations of the focal points. What do you observe?
Q2. What happens when the length of AB is greater than the length of F1F2? Why?
Finish this activity before clicking here.