Overview of Section 4.2 Applications of Side-Splitting Theorem and Similarity.
Theorem 4.7
If an interior angle of a triangle is bisected, the bisector divides the opposite side into segments whose lengths are in the same ratio as the lengths of the other sides of the triangle. That is, if AD is the angle bisector of angle A in triangle ABC,
Open GSP file for Theorem 4.7 and its proof.
Extra:
What is the locus of the vertex A if base BC is fixed and triangles ABC are constructed so that the ratio of AC to BC is fixed? That is, prepare a GSP animation such than for a base BC, AC = kAB. Does your construction work for k = 1?
Theorem 4.8:
If an exterior angle of a triangle is bisected, the bisector divides the opposite side externally into segments whose lengths are in the same ratio as the lengths of the other sides of the triangle.
That is, if AD' is the angle bisector of the external angle at A in triangle ABC, then
LEMMA: The internal and external bisectors of at an angle of a triangle are perpendicular.
Proof: The sum of the internal angle and the external angle is 180 degrees. The angle between the internal and external bisectors is the sum of one-half of each. Therefore the angle measures 90 degrees.
Harmonic Division of a line Segment.
Definition:
A line segment AB is divided harmonically in a given ratio
≠ 1 by determining two points, one internal H and one external H' such that aH' = bH. That is
Construction: Given a line segment AB. Represent the ratio
Construct a GSP file to implement this construction. You may want to create a script tool and save it on your comput3er or your web site.
(An alternative construction is given in the textbook.)
PROBLEM: How can this construction be accomplished if a + b < AB?
Answer: Use ka and kb.
PROBLEM: What if a = b? That is,
The Circle of Apollonius
Other web sites of interest --
EMAT 6600 Circles of Apollonius
Cut-The-Knot Locus of Points in a Given Ratio to Two Points.
Wikipedia Apollonius's Alternative Definition of a circle.
Apollonius discovered that a circle could also be defined as the set of points P that have a given ratio of distances k = d1/d2 to two given points. These two points are sometimes called the foci.
Theorem 4.9
The locus of all point P for which the ratio of the distances from two fixed points A and B is constant is the circle of diameter DD', where D and D' divide AB harmonically in the ratio of that constant.
Discuss: What is to prove? Given a segment AB and a ratio m, we want to explore the set of points P such that m(AP) = BP. We can construct a triangle ABC with AC = mBC. From that we can divide the segment AB harmonically by the ratio m and find points D and D' by the interior and exterior angle bisectors at C. These angle bisectors for a right angle and so with the midpoint of DD' at M, we can construct a circle of with diameter DD' with will contain D, C, and D'.
Now, the we need to prove that any point P we locate on the circle will have AP = mBP.
Now Solve This 4.7
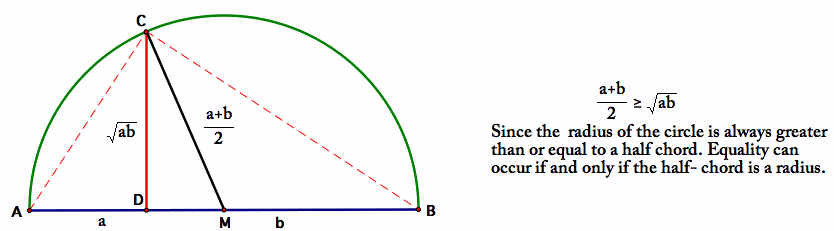
Using the figure above (not the one in the textbook), MD is the radius of the Circle of Apollonius on segment AB, prove that
This result shows that if a segment AB is divided harmonically, then the Circle of Apollonius is a circle of inversion mapping A to B and vice versa. We will be looking at the geometry of inversion later.
Similarity of Right Triangles
The next theorem is one of the most elementary and useful theorems about right triangles.
Theorem 4.10
In a right triangle, the altitude to the hypotenuse is the geometric mean of the segments into which it divides the hypotenuse.
One interpretation of the geometry mean is that it is the length of the side of a square with area equal to the area of a rectangle with sides of length a' and b'.
EXTRA: Prove the converse of Theorem 4.10 -- if AB is the side of a triangle divided into segment a' and b' and h is the geometric mean of a'and b', then show that the triangle ABC with altitude h is a right triangle.
Construction of the Geometric Mean
Theorem 4.10 gives a suggestion for constructing the geometric mean given two segments of length a and b. We will construct a triangle with hypotenuse AB of length a + b such that AD = a and BD = b. Since a + b is the length of the hypotenuse, we can take the midpoint of the hypotenuse and construct a semi-circle (or a circle) with radius one-half the hypotenuse. Point C must be on that circle but point C is also on the perpendicular from D. Therefore construct the perpendicular from D to find C. By Theorem 4.10, h is the geometric mean of a and b.PROOF of Arithmetic Mean-Geometric Mean Inequality
Theorem 4.11:
If two chords intersect in the interior of a circle, then the product of the lengths of one chord equals the product of the lengths of the other chord. Each product equals
where r is the radius of the circle and d is the distance from the point of intersection of the chords to the center.
