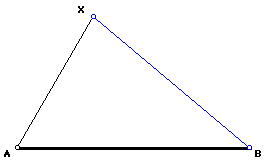
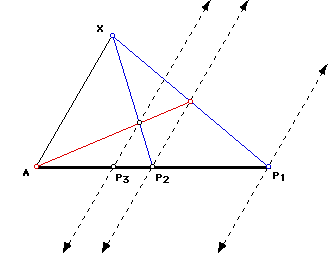
Construct AX and XB.
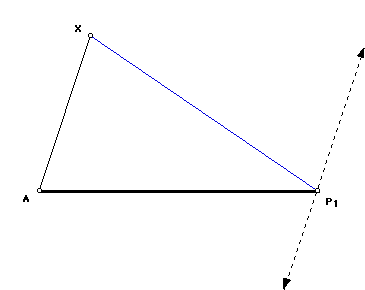
The line parallel to AX through B cuts off 1/1 of AB. Label B = P1.
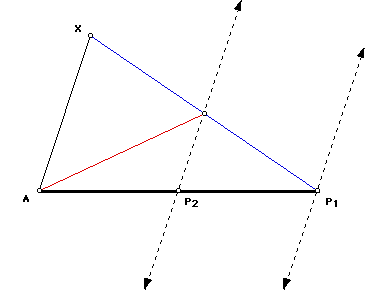
Construct the median from A to XB. Construct the parallel to AX through
M. The parallel cuts of a segment that is 1/2 of AB. The point P2 is a midpoint
of AB.
Now XP2 is a median of the triangle and the point of intersection is
the centroid. Therefore the line parallel to AX through the point of intersection
cuts off a segmet AP3 that is 1/3 the length of AB.
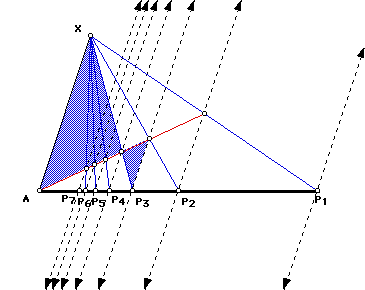
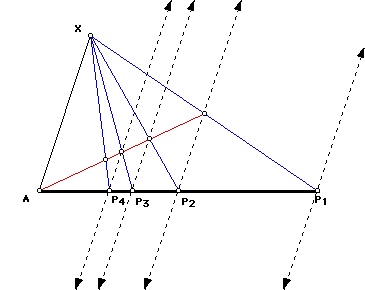
The procedure can be continued to locate P4, P5, P6, P7, etc. Similar
figures, such as those shaded for P4, can be use to prove the construction
from Pn-1 to Pn.
-