
Department of Mathematics Education

by Jim Wilson, University of Georgia.
Divide any line segment into a regular partition of any number of partsby Dan Litchfield and Dave Goldenheim with support from Charles H. Dietrich.
Part 1
Part 2
A GSP Sketch
A revised presentation of the GLaD construction results from using the line segment AM as the diagonal of the rectangle, resulting in the following figure and the corresponding simplification of the presentation. This change was mentioned on the GLaD Web Page.
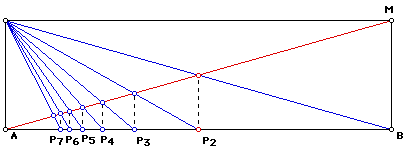
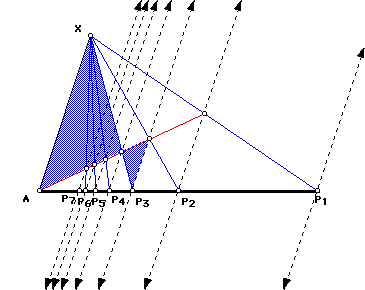
Construction
A proof follws readily at each stage considering the similar triangles and
the ratio of similarity in each case. All this is very similar to "moving
M to C." It presents a single sequence for all cases rather than separate
ones for odd and even segmentations.
See The SaRD Construction: An Elegant Solution
for Euclid's Partitioning Problem.
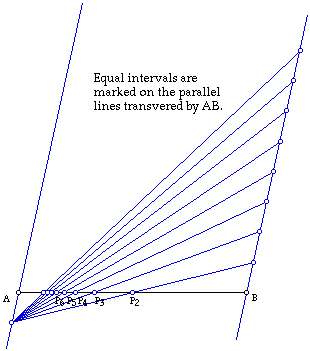
Leslie, of course, accompanies his discussions with proof. The process
also leads to a strategy for dividing a line into n equal parts. It is quite
like the SaRD construction
Leslie then presents the drawing below
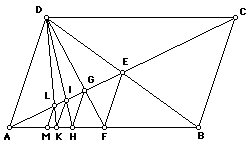
constructed and proved that the segments AF, AH, AK, AM are the half,
third, fourth, and fifth parts of the segment AB. This is very similar to
the GLaD construction.
On page 424, Note XXXVIII, Leslie comments on the material on pages 150-153
as follows:
The consideration of diverging lines furnishes the simplest and readiest means for transferring the doctrine of proportion to geometrical figures. The order in which Euclid has followed, beginning with parallelograms, and thense passing from surfaces to lines, appears to be less natural.On page 425, Note XXXIX, Leslie comments
It is will be proper her to notice the several methods adopted in practice for the minute subdivision of lines. The earliest of these -- the diagonal scale -- depending immediately on the proposition in the text is of the most extensive use ..."The GLaD construction as presented by Dan Litchfield and Dave Goldenheim is a marvelous accomplishment. The fact that it has been around in some form for a very long time should not detract from the rediscovery and modern presentation they have given.