Capturing Area and a Solution

by

Lyle Pagnucco
University of Minnesota - Duluth

and

Jim Hirstein
University of Montana


The intent in writing this paper is to document events when two problem solvers work collaboratively in the pursuit of a suitable model and solution. We were simply trying to build a solution to a relatively simple problem that became a phenomenon. The phenomenon emerged when we realized our discoveries begged for us to question and generate a general case. We attribute the phenomenon to our interaction with each other, the technological tools we used, and the reflection time between contacts. An alternative exploration with this same problem environment is given by Wilson (1996).

Why is the solution of this problem so important? Perhaps because the events illustrated here reflect the sequence that actually took place and appear inconsistent with strategies used in traditional instruction but consistent with NCTM (1989) recommendations. Traditional instruction often provides a "sanitized" version of mathematics that is logically correct and summative in nature but not always representative of the events leading to a solution. This is an opportunity to illustrate how rich a problem solution becomes if problem solvers allow their web of resources to become an integral part of problem solving. Clearly, we use many traditional events to help build our solution but we also sensitize ourselves to synthesize technology and heuristics into important contributors to the overall solution.

When providing models in support of explanations, especially in mathematics, it is often difficult to build or match models to the actual problem. This particular instance is a case where we chose a geometric problem and in the course of pursuing a solution iterated our methods from an static model to a series of dynamic models. The iteration resulted from and was motivated by a lack of satisfaction with a static model, especially the narrowness of the solution.

The original problem asked for the shaded area captured between oblique segments as illustrated in Figure 1. Our data consisted of; ABCD a square of side 2 inches, and G the midpoint of AB. The oblique segments were connected from each vertex to the midpoint of one non-adjacent side.


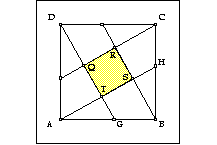
Figure 1

Our first reaction was to analytically determine the area by using what we knew about similarity and, naturally, we focused on the following algebraic/geometric method.




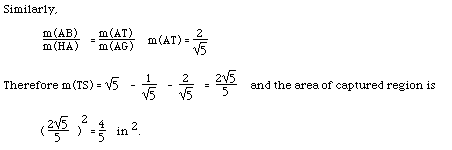
So, we have an answer and what may be considered a complete solution. Clearly, this is a paper trail leading to a numeric answer where organization and logic are important but this single case leaves many questions unanswered.

There are many more such questions but it is not our intention to address all of them directly. We intend to hold the dimension of the square to 2" and iterate our explanation to a general case when the endpoint of segment DG is anchored to any point on the side of square ABCD. In this case, the variable distance AG could have been assigned x and appropriate substitutions in our numerical solution would suffice to result in a defining function but we chose not to follow that path. We considered our numerical model was sufficient but it did not provide physical evidence of relative size and movement if G was to travel along AB. Our choice was to build a geometric model which allowed access to those two attributes. We needed technological tools so we reverted to Geometer's Sketchpad software.

The Geometer's Sketchpad model in Figure 1 allows point G to float along segment AB and also facilitates data collection through a tabulation feature. We decided point G should move from point A where m(AG) = 0 to B where m(AG) = 2 and during the process collect measures (Table 1) of side TS and the area of QRST.

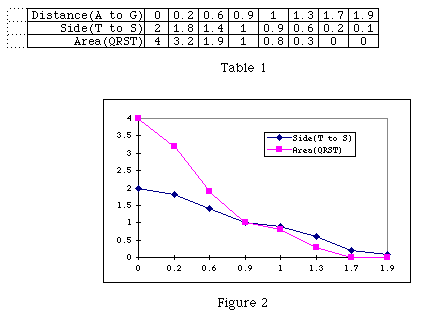
As G moves along segment AB, side TS and the captured area decreases. We tried to predict the nature of these decreases. This notion emerged from our discussion regarding the selection of points where data was collected. We made no attempt to collect data at uniform distances nor were we particularly concerned about precision at this point. The data poorly illustrated rate of change so our next move was toward a graphical illustration (Figure 2). It was clear, at least under the level of precision we used and from Figure 2 neither the side nor area of the captured region changed at a constant rate.

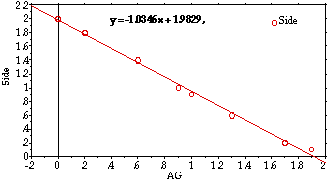
Recall, we had not yet looked at the algebraic model for this phenomenon. We assumed the irregularity of side measures was attributable to the level of precision set within the software. With this in mind, we assumed a constant rate of change for the side measure but our intuition left us with a suspicion further investigation was required.


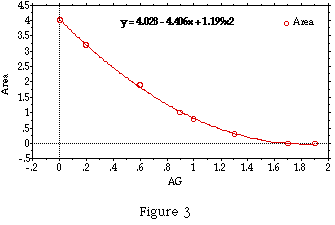
Likewise, we assumed quadratic definition for the rate of change of area for two reasons. First, the plot in Figure 2 approximated a segment of a parabola and second, area is considered the product of two linear conditions. Our graphical model in Figure 2 left us with a decision about whether our representations were precise enough and whether our assumptions were justifiable. We had two choices to help determine whether our assumptions were on line. One choice was the creation of a curve of best fit for each set of data and compare the results found from their algebraic definitions. The second choice was a more efficient choice, it called for the development of defining functions for side measure and area from the our original numerical solution. We knew which choice was most efficient but we wanted to authenticate our assumptions, so we chose to find curves of best fit (Statview) and their corresponding functional definitions.

Statview software regressed to a linear function representing the measure of side and a quadratic function for area. In both cases, the algebraic models were rather precise (mean error 0.0005). Under normal circumstances this solution may have been accepted as complete but as we said earlier our intuition about fairness of representation and precision led us to ask a follow-up question. How fair are algebraic and geometric models if we choose to extend AG beyond B in a positive direction and beyond A in a negative direction? There were some clear problems. The geometric model indicated as AG grew beyond B to the right there was a point where area and side increased in size but tended to a limit. This was the first inconsistency since our models (linear, quadratic) indicated unbounded side and area measures as AG increased. Similarly, as G moved beyond A to the left there was also an upper limit for both side and area measures. In addition, the rate of change of side and area measures appeared different if one were to compare the activity of the geometric model when G was moved left or right. Clearly, our curves of best fit were useful but limited.
So the concern for a higher degree of precision and fairness led us back to the derivation we developed in answering the original question. We assigned x to represent the value of m(AG), s(x) to represent the side measure, and f(x) the area of the captured region QRST. The following s(x) and f(x) resulted.




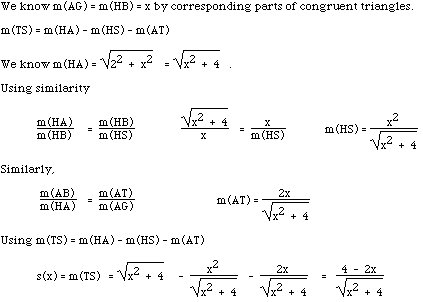
It is immediately clear these functions are not of linear or quadratic form so we decided to correlate our collected data to values generated from s(x) and f(x) and found r = 0.9995. Again, we were satisfied with the precision and now more confident about the fairness of our model. The basis of our confidence was rooted in the logic of our symbolic derivation and the improved correlation. We felt our confidence would greatly increase if we could make predictions beyond the interval . This led to a next phase of our solution by releasing the restriction of G to the side of a square. Why not let G ride along a line AB? The first test was to use our improved s(x) and f(x) and plot them over a domain which resulted in Figure 4.

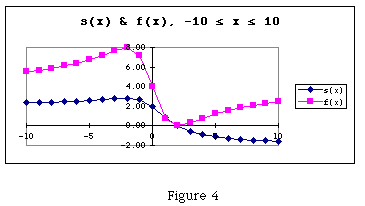
The plot of s(x) indicates an increase in s(x) from x = -10 to x = -2 and then there is a relatively sharp drop to where s(x) = 0 then it somehow becomes negative. Once s(x) becomes negative it appears the rate of change in s(x) decreases and possibly approaches a limit. Figure 4 promotes many questions. What does a negative s(x) (side measure of the captured region) mean? Is there a limiting value for s(x) and if so what is the value? In a likewise fashion, f(x) increases from x = -10 to x = -2 where a maximum occurs and then decreases at a quicker rate to a minimum of f(x) = 0 when x = 2. Once past x = 2, f(x) increases and also tends to a limit. This is consistent with what happened to s(x) and if the side of the captured region tends to a limit it is reasonable for the area captured to have the same characteristic. As with s(x), the graph of f(x) suggests questions such as:

The algebraic and graphical representations told a story but the newly generated questions certainly had merit and we felt deserved pursuing. We felt there was a compelling reason to push one step further. If software permits a pictorial model then why not build more confidence into our algebraic and graphical models with a geometrical model. The original Geometer's Sketchpad model was altered to accommodate the movement of G and the sequence of pictures in Figure 5 resulted. The questions addressed through the extended Geometer's Sketchpad model aimed at addressing the questions:

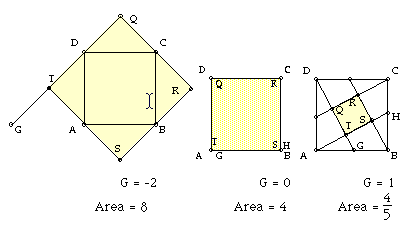
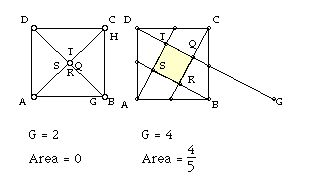
The sequence of pictures illustrates a shrinking captured region where the side measure shrinks to zero then re-emerges. Curiously, side QT emerges as side TQ and on what appears to be the opposite side of the captured region. Is this what happens when a side measure is represented by a negative number? Clearly, there is a transformation in this physical model and the mathematics here is telling the problem solver to be aware of some phenomenon.



Figure 5

The second question, Is there a limiting value for s(x) and if so what is the value?, can also be addressed and with varying degrees of sophistication. A less sophisticated discussion may only include a comparison of pictures representing areas of 4/5. In one case (G = 1), G is only one unit from where area = 0 and in the second case (G = 4), G is 2 units from area = 0. This suggests that it has taken s(x) a longer time to grow back to its previous size. In addition, when the model was extended such that G moved a great distance from A the data in Table 2 resulted.

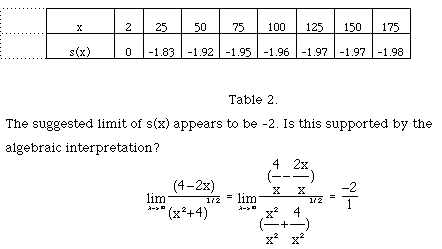
What about the question relating to area (f(x))? Can a maximum area of 8 be justified? Justification of a maximum area can be a calculus or geometrically supported case. From calculus, recall the notion of using a first derivative set to zero (the regions on a curve with zero slope).



Figure 6.

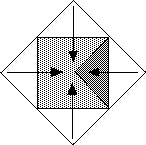
This is normally the practice when such a question is asked but in our case the geometric model illustrated just one case when the captured area had an area at 8. To reaffirm the area was 8, we flipped in the flaps indicated in Figure 6. This provides sufficient evidence for current purposes.

If there is a story to be told then it seems the focus here was based on the construction of a net of observable and justifiable connections. There are many more questions, answers, and justifications to be found in such a problem but the important factors are the generation of ideas promoted by collaborative efforts and the understanding needed to connect models used to communicate mathematics. Some models seem fair but limited. It is important to recognize limits and extensions when necessary and there must be a willingness to deviate traditional solutions. Maybe, technological tools need to be used as vehicles for illustration and provocation that enrich mathematical solutions. State and national Standards recommend richness of solution for future school mathematics so it seems appropriate to use what we know and question where it fits in coming to better understand what is learned. This suggests understanding mathematics based on at least two levels. One level recognizes detail and logic holding a solution together and the second level, suggests a more holistic view. A view that locates a problem solution in a context and illustrates inter and intra relationships between elements of the solution and that context.

Reference

Wilson, J. W. (1996) Squares. Http://jwilson.coe.uga.edu/squareF/square.html.
Return