
Mathematics Education

We begin with a simple problem. Given a square of side s and segments drawn from each vertex to the midpoint of the second side, counting counter-clockwise, as shown at the right.
The segments intersect to form a new square.
What is the ratio of the area of the shaded square to the area of the original square?
An alternative discussion of explorations with this problem is given by Pagnucco and Hirstein (1996).
Technology tools such as Geometer's Sketchpad allow direct measurement of the areas and computation of the ratio. This strategy is fine if its purpose is to discover relationships and work for a solution based on reasoning.
Perhaps a "teachable moment" is here to discuss that in fact the shaded figure is a square; why are pairs of segments parallel and mutually perpendicular? I will leave this for the moment as "clear." An alternative statement of the problem could incorporate these things into the problem.
I want to address some strategies to examine this problem and to extend it. I have used this problem for years in my Problem Solving course and I would be hard pressed to document an original source. I have seen (and used) the gamut of bonehead to insightful approaches. I have seen frustrated students who wanted to solve but could not; I have seen students who were not frustrated since they did not find the problem interesting enough to work on it.A common thread I find in student solutions to this problem is the premature lust for using algebra -- to get quickly to computation and circumvent thinking. Often this leads to complicated algebraic solutions using the Pythagorean relationship. Insightful use of the Pythagorean relation and a little algebra CAN lead to an elegant solution. Click HERE to see that approach.
A closely related strategy is to particularize the data -- for example let the original square have an area of 4 (i.e. sides of lentgh 2) and find a way to compute the area of the shaded square. In this case the we have AF = 5 and the geometry can tell us AF is divided in the ratio 2 : 2 : 1. .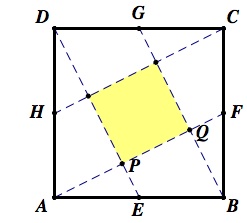
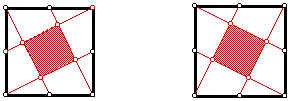
Let us explore the problem a bit with geometry. By drawing lines along and parallel to the segments within the square, a grid overlapping the original square is produced. If A represents the area of the shaded square, then 9A represents the area of the circumscribing square with sides parallel to the shaded square.
It is easy to see a right triangle on each side of the original square with its hypotenuse on the side of the original square, each with an area of A. Thus the total area of the original square is 5A, or the ratio of the area of the shaded square to the original square is 1/5.
Alternatively, we could note that the small right triangle to the inside of one half of each side of the original square is congruent to the small right triangle on the outside of the other half of the side. This can be seen by considering a 180 degree rotation of the internal triangles about the midpoints of the sides.
or, we can see that the area of the original square is equal to the area of this five unit cross:
Although this is a neat way to look at the problem with the sides are divided in half, it does not generalize when the sides are divided into more that two equal parts. On the other hand the grid strategy can be adapted to the more general cases.
AN ALTERNATIVE (geometric)
It is relative easy to dissect the configuration into a set of 20 congruent right triangles. The square in the center is covered by 4 of these congruent right triangles. Thus the ratio of the area of the yellow square to the original is 4 to 20, i.e., 1 to 5.
We should explore whether this dissection stragegy will generaize to extensions of the problem.
EXTENSIONS OF THE PROBLEM
For the first extension of the problem and the strategies, let us consider the points on the sides of the original square dividing each side into thirds. It appears that the ratio of the internal square to the original will be larger than when we divided each side in halves.
One placement of a grid across the configuration shows the shaded area as follows:
Now, the area of the shaded square is four grid units; the area of smallest circumscribing square is 16 grid units; the area of each of the right triangles on each side of the original square is 3/2 grid units, or a total of 6 grid units in the four right triangles. The ratio of the areas is 4 : 10, i.e., 2 : 5.
With the dissection alternative, we would have the original square covered by 60 congruent right triangles and the yellow square covered by 24 of them. Thus the ratio of the area of the center square to the area of the original square is 24 : 60, i.e., 2 : 5.
The cutting of the side of the original square into 3 parts rather than 2 results in twice the area in the center square.
In another extension, a shaded square is created by taking points 2/3 the distance along each side rather than 1/3.
Completing a grid over the figure is shown at the right.
The area of the shaded square is one unit of the grid. The
four right triangles built around the shaded square each has an
area of 3 grid units. Thus the area of the original square is
13 grid units and the ratio is 1/13.
It is time to look for some generalizations. Let us divide each
side into b lengths (b > 1) and divide each side by taking
a of the lengths. Thus the points on each side cuts off the fraction
a/b of the units. If we are not ready for this generalization,
we could test a few more specific cases, such as 1/4 and 3/4
The respective ratios are 9/17 and 1/25.
Lets examine the case where a/b = 5/9.
There are 16 grid units in the area of the shaded square. Each right triangle to complete the square has area of (5)(9)/2 or 90 grid units in the four triangles. Thus the ratio is 16/106 or 8/53.
So far, for any fraction, we have counted the number of grid units in the shaded square. For a/b the number of grid units in the smallest circumscribing grid is
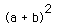
The number of grid units in the four right triangles around the shaded square is 2ab. The number of grid units in the original square is
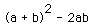 .
.
Thus the number of grid units in the shaded triangle is
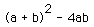
and the ratio of the area is
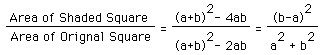
Check: for
The formula is also consistent with the physical situation which finds the ratio goes to 0 when a = b and the ratio goes to 1 when a = 0, b > 0.A FURTHER EXTENSION
Now, what if a > b? For example, let a/b = 4/3.
The shaded square is still formed and its area here is one grid unit. The ratio of the shaded area to the area of the original square is 1/25. The ratio is the same as the case when a/b = 3/4.
It is also clear from the geometry that as a gets larger and larger (with b fixed) the ratio of the areas approaches 1.
AND, ANOTHER EXTENSION
What about when a < 0? The first step would be to give a physical interpretation. Counting the units in the negative direction seems logical. The construction of the grid with such an interpretation of a shows that the shaded square will circumscribe the original square. For example, if a/b = -1/3, we have the result on the right.
Completing a grid gives this.
Clearly, the shaded square is defined by our construction rules and the ratio of the area of the shaded square to the area of the original square is greater than 1. Also, the area of the shaded square is 16 grid units and the area of the original square is 10 units. The ratio is 16/10 or 8/5. This value is also confirmed by the formula when a = -1 and b = 3.
The ratio when a/b = -2/3 is 25/13, confirmed by using either the grid or the formula. When a= -3 and b = 3, the area of the shaded circumscribed triangle will be twice the area of the original triangle; for a < -3, b = 3, the ratio will always be greater than 1 (because the shaded square circumscribes the original) and less than 2.
Another GSP construction and animation, with measurements, shows how the ratio varies as the distance varies along a line placed on one side of the original square.
Some algebra
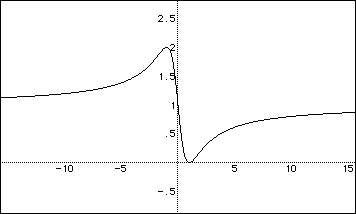
Now, at last I am willing to move to algebra to provide some summarization and generalization. Let x = a/b. x is therefore the directed distance from a corner of the original square. Then by substituting a = bx in the formula, we have the function at the right
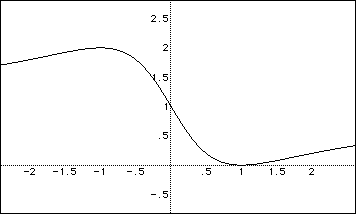
Using any function grapher, with f(x) for the ratio and x for the distance from the lower left corner of a unit ssquare as the original square, shows graphs such as the following.
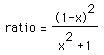
Summary.
Let x be the distance from the lower left corner of the original unit square. Then
As x goes from 0 to 1, the ratio of the areas goes from 1 to 0. At x = 1/2, the ration is 1/5; at x = 1/3 the ratio is 2/5. etc. We could also ask: For what value of x would the ratio be 1/2? 1/10? etc.
As x goes from 1 to a very large number, the ratio always increases but is between 0 and 1. Thus as x gets large, the ratio approaches 1 as a limit but is always less than 1.
As x goes from 0 to - 1 the ratio increases from 1 to 2. It reaches a maximum at x = -1. From x = -1 to |x| very large, the area is decreasing but always greater than 1. Thus in the negative direction beyond x = -1, the ratio approaches 1 from above.
The range for the ratio k is from 0 to 2. For any value k in this range other than 0 , 1, or 2, there are two values of x that will yield this value of k. If k is 0, 1, or 2 the yield is one value of x corresponding to the minimum ratio (x = 1), the unit ratio (x = 0), and the maximum ratio (x = -1). If k is between 0 and 1 then both values of x are positive (one less than 1 and one greater than 1 -- and reciprocals. See the Corollary below); if k is between 1 and 2, then both values of x are negative (one between 0 and -1, the other less than -1).
Extension. What if?
Go back to the original problem. What if all eight of the segments from a vertex to the non-adjacent sides of the square had been drawn? An octagon would have resulted. What is the ratio of the area of the octagon to the area of the original square?
It would be easier if this turned out to be a regular octagon, but it did not. Does anything we have learned from the original problem help with this extension?
Here is the analogous problem of an octagon when the sides are divided in thirds.
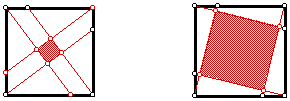
A corollary.
When the shaded square is constructed we could have drawn the internal segments moving either counterclockwise or clockwise around the square, producing two different shaded squares. For a/b other than 1/2, what is the relationship between the two?
Reference
Pagnucco, Lyle, & Hirstein, Jim (1996) Capturing Area and A Solution. Http://jwilson.coe.uga.edu/texts.folder/Pag/hirpag.html.