
Side b and median b and median a
By: Tim Lehman

Given:

First, trisect m(a) and m(b). Click here if you need help trisecting a segment. We know the centroid is 2/3 of the length of m(a) away from vertex A. Also, the centroid is 1/3 of the distance of m(b) away from the midpoint of side b. Thus, the centroid (point X below) is at the intersection of the two circles centered at A and the midpoint of b with a radius of 2/3 of m(a) and 1/3 of m(b), respectively. So, to start the construction, we draw side b and the two circles.
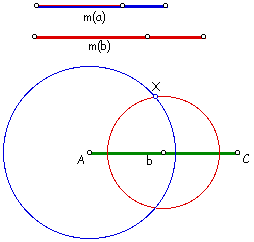
Because both medians must go through the centroid, we can now draw both medians. Further, by definition, the endpoint of m(b) must be the vertex B. Therefore, we can construct the triangle.
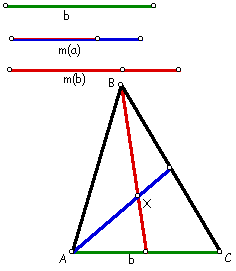
Click here for a GSP sketch.