
How to trisect a segment
Tim Lehman

A segment can be trisected in many ways. Most of the methods use similar triangles in some way. Below, two different ones are found. The first is a traditional trisecting of a segment. The second construction has the advantage of relying solely on the endpoints of the segment we want to trisect.
Method 1:
When trisecting a segment AB, first we want to draw the ray AC.
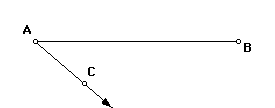
Next, we will draw a circle center at C and passing through A. Let the intersection of the circle and ray (AC) be point D.
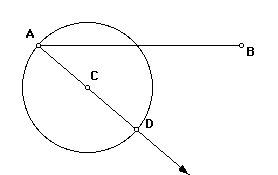
Construct the circle centered at D and passing through C. Let the intersection of this circle and ray (AC) (that is not point C) be point E. Points C and D now trisect segment AE.
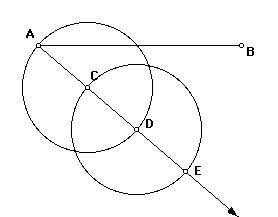
Construct segments EB and AE. To clear up the picture, we will now hide the two circles and ray AC.
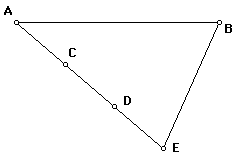
Construct segments DF and CG such that points F and G are on segment AB and DF and CG are both parallel to BE.
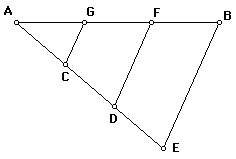
By construction, triangles ACG, ADF, and AEB are all similar. Further, AC=1/3AE and AD=2/3AE. Thus, AG = 1/3 AB and AF=2/3AB. Because
AG + GF=AF, it follows that GF=1/3 AB as well. From the fact that AF=2/3AB, we can also note that FB=1/3AB. Therefore, segment AB is trisected by points G and F.
Method 2
The second method has the advantage of not needing an auxillary point (like point C in Method 1). Thus, a GSP script or tool could be created that uses only the endpoints of the segment AB.
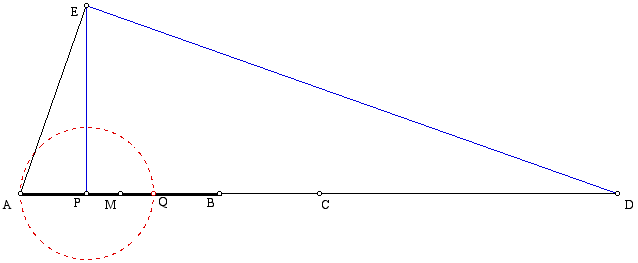
Construct segment AB and its midpoint M. Then, construct the circle centered at B and passing through M. Let C be the point where the circle intersects line AB.
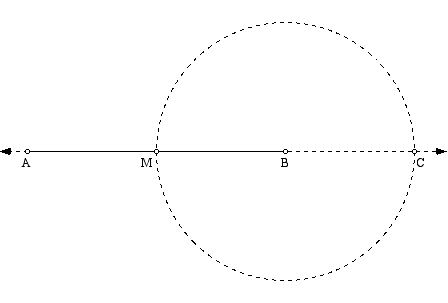
By construction, AM=MB=BC. Thus, AC=3/2 AB. Construct the circle centered at C and passing through A. Let D be the intersection of this circle and line AB. Thus, AD=2(3/2AB)=3AB.

Construct the circle centered at A and passing through B. Let E be the point of intersection of this circle and the circle in the last part. Next, construct the line perpendicular to line AB and passing through point E. Let the intersection of this perpendicular line and line AB be P. Thus, by construction, AE = AB.
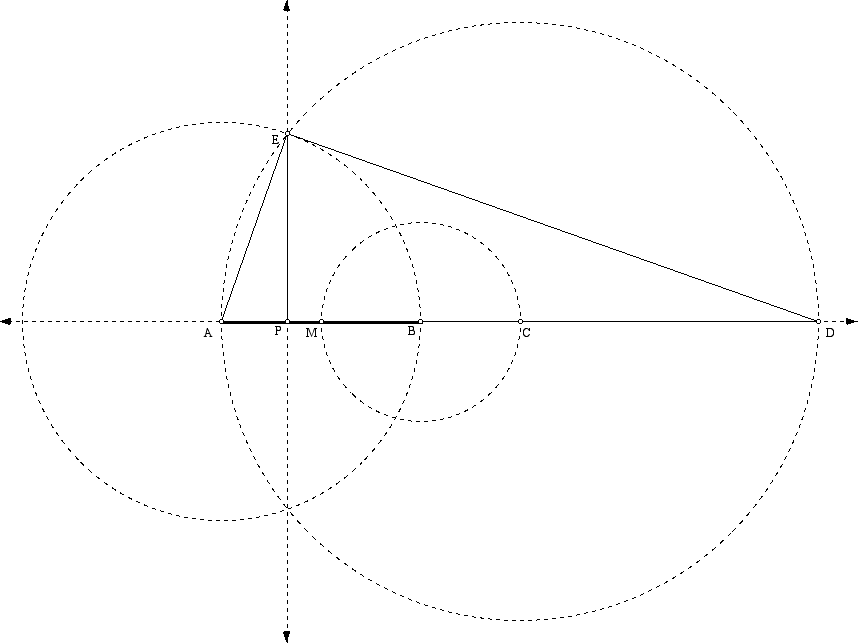
After cleaning up some of the construction lines, we have the following drawing.
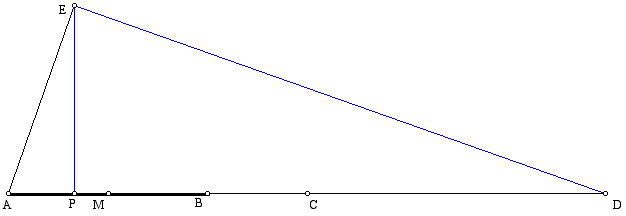
It is known angle (AED) is a right angle because the angle is inscribed in a semicircle. Also, angle (APE) is a right angle by construction. Because angle measures made by the same rays are the same angle, angle (EAP) = angle (DAE). Thus, triangle (EAP) is similar to triangle (DAE) because their corresponding angles are equal.
Above, it was noted AE = AB and AD = 3 AB. Thus, AD = 3 AE. The ratio of the corresponding sides of the two similar triangles must then be 1:3. This would mean that
3AP = AE = AB. AP is therefore 1/3 of AB. By constructing a circle centered at P and passing through A, we can create another point Q that is 2/3 along AB. Thus, P and Q trisect AB, as desired.
Return
to Triangle Trisection
Return
to Triangle Constructions: Side and Two Medians