

![]() Click check to check your
problems from Trigonometry.
Click check to check your
problems from Trigonometry.
Right triangle geometry has many applications in the real world. Carpenter use it to make cabinets, surveyors use it in their work, you can use what you've learned to measure tall structures. In this lesson you will use what you have learned to solve problems.
Steps for solving "word" problems:
1. Read the problem all the way through.
2. Read it again, drawing a picture of whatever you can.
3. Label the picture with all that is given.
4. Write down any givens not already in the picture.
5. Write down what you want to find out (the unknown).
6. Use any formulas in this lesson to write the unkown in terms of what is given.
7. Solve for the unknown using algebra.
Below I will use the steps outlined above to solve some examples.
The first example involving surveying, uses the altitude of a right triangle thereom:
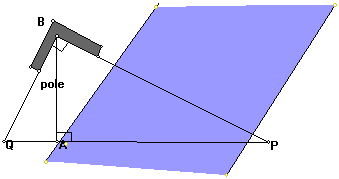 Laura uses a carpenter's square to find the distance
across a river. She put the square on top of a pole which is high enough
to sight along a straight line from one of the legs of the carpenter's square
across the river to point P. She then sights along the other leg of the
carpenter's square in a straight line to a point Q. If QA is 2 feet, and
BA (the pole) is 6 feet, find AP.
Laura uses a carpenter's square to find the distance
across a river. She put the square on top of a pole which is high enough
to sight along a straight line from one of the legs of the carpenter's square
across the river to point P. She then sights along the other leg of the
carpenter's square in a straight line to a point Q. If QA is 2 feet, and
BA (the pole) is 6 feet, find AP.
Solution: First we will put the givens on our picture :
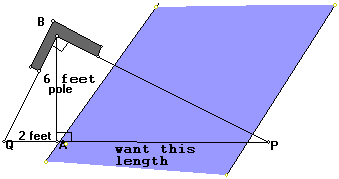 Next, since we ghave an altitude of a right triangle
to its hypotenuse and we are looking for on of the pieces of the hypotenuse
I will look at part a of the right triangle altitude theorem:
The measure of the altitude drawn from the vertex of the right
angle of a right triangle to its hypotenuse is the geometric mean
between the measures of the two segments of the hypotenuse.
Next, since we ghave an altitude of a right triangle
to its hypotenuse and we are looking for on of the pieces of the hypotenuse
I will look at part a of the right triangle altitude theorem:
The measure of the altitude drawn from the vertex of the right
angle of a right triangle to its hypotenuse is the geometric mean
between the measures of the two segments of the hypotenuse.
So I can write an equation between the knowns and unkowns. By the definition
of geometric mean I have 
Note: always carry your units throughout a problem. If your units don't check out when you are done then you know you made a mistake somewhere.
The Smith's bought a 6-ft-square sheet of plywood as a base for their electric train. Will the plywood fit in the back of their van? The opening of the van is 44 inches high and 60 inches wide.
First we read the problem.
Next draw a picture that describes the problem: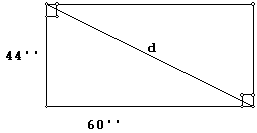
We know the diagonal will be the longest length, thus if the plywood is to fit, the diagonal must be greater than 6 feet. We have a right trianngle, and d is the hypotenuse. We know the length of both legs so we can use the Pythagorean Theorem to solve for d.
The Pythagorean Theorem states that the sum of the squres of the legs
of a right triangle is equal to the square of the hypotenuse. We would have:
So the plywood would fit
Again pay carefull attention to your units!
The airport meteorologists keep an eye on the weather to ensure the safety of the flights. One thing they watch is the cloud ceiling. The cloud ceiling is the lowest altitude at which solid cloud is visible. If the cloud ceiling is too low the planes are not allowed to take off or land.
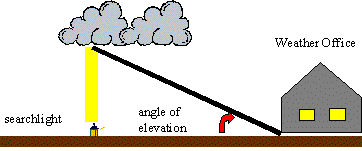 One way a meteorologist can find the cloud ceiling
at night is to shine a searchlight that is located a fixed distance from
their office vertically into the clouds. Then they measure the angle of
elevation to the spot of light on the cloud. The angle of elevation is the
angle formed by the line of sight to the spot and the horizontal. Using
trigonometry, the cloud ceiling can be determined.
One way a meteorologist can find the cloud ceiling
at night is to shine a searchlight that is located a fixed distance from
their office vertically into the clouds. Then they measure the angle of
elevation to the spot of light on the cloud. The angle of elevation is the
angle formed by the line of sight to the spot and the horizontal. Using
trigonometry, the cloud ceiling can be determined.
Example: A searchlight located 200 meters from a weather office is turned
on. If the angle of elevation to the spot of light on the clouds is ![]() , how high is the cloud ceiling?
, how high is the cloud ceiling?
First read the problem
Now draw a diagram of the problem: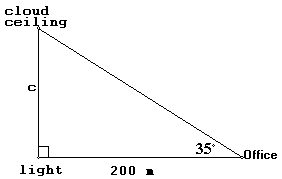
Let c be the cloud ceiling, what we are looking for.
We know the length of the side adjacent to the given angle , and are looking for the side opposite the given angle. What trigonometric ratio involves these two sides?
![]()
So we can write the unknown in term of the known. Then using algebra
we solve: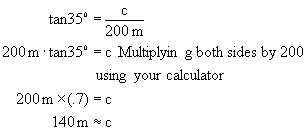
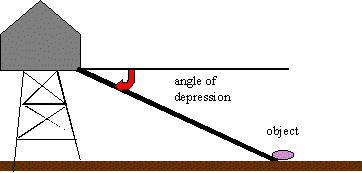 Note: Angle of depression occurs when the line of
sight is above the object:
Note: Angle of depression occurs when the line of
sight is above the object:
 Click the lightbulb
to practice what you've learned.
Click the lightbulb
to practice what you've learned.