---

---

---

Checkerboard Problems

---

       Lines intersecting regions

           1. Draw a line across a 4 x 5 checkerboard so that the maximum number of regions are intersected.

Case 1: A line through a corner point is in all four regions

Case 2: A line must go through an interior point of the region to claim that it intersects the region

            2. Extend to an m x n checkerboard.

     Number of squares or rectangles of any size on a checkerboard.

           1. How many squares of any size are in an 8 x 8 checkerboard?

           2. Extend to an m x n checkerboard.

           3. How many rectangles of any size on an m x n checkerboard?

      Number of squares by lattice points

           1. Given only the lattice points (points where four of the squares in a grid will meet), how many squares of any size can be found on a 5 x 5 grid? For example,

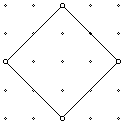
          2. Extend to an m x n grid.

          3. Given only the lattice points of an n x m grid where n and m are very large, can you draw a linethrough the grid which intersects no lattice points, only one lattice point, only two lattice points?

          4. Answer question 3 for m and n both infinite.

       EXTENSION

        Make up your own problem or problems related to a checkerboard or lattice grid.