

by
JIM WILSON
A Presentation to the Annual Meeting of School Mathematics and Science Association, Birmingham, November 8, 2012, was prepared using some parts of this paper.
The Arithmetic Mean-Geometric Mean Inequality (AM-GM Inquality) is a fundamental relationship in mathematics. It is a useful tool for problems solving and building relationships with other mathematics. It should find more use in school mathematics than currently. It what follows I present an introduction to the theorem, some background and generalizations, alternative demonstrations of the proof, and examples of problems that can be explored by using the AM-GM Inquality. I will rely heavily on a collection of problems and essays on my web site:
and the sub-directory for my mathematics problem solving course at the University of Georgia.
I will concentrate on the theorem for two positive numbers in my examples, but I mention the generalizations below and occasionally use the case for three positive numbers.
Arithmetic Mean - Geometric Mean Inequality
For real positive numbers a and b, the AM-GM Inequality for two numbers is:
Clearly, the AM-GM Inequality can be generalized for n positive numbers. The link poses the problem of generalizing the proof following the lines of argument advanced by Courant and Robbins (1942). That is,
The AM-GM Inequality can also be generalized to its inclusion in relation to other means such as the Harmonic Mean (HM) or the Root Mean Square (RMS -- sometimes called the Quadratic Mean). In particular, for two positive numbers a and b,
At a more advanced level (perhaps more fundamental?) all of these means are instances of Power Means where the power parameter p takes on different values for the different means. These may also be called Generalized Means.
What is the Value of this Theorem? An Example.
The AM-GM for two positive numbers can be a useful tool in examining some optimization problems. For example, it is well known that for rectangles with a fixed perimeter, the maximum area is given by a square having that perimeter.
Ed. Comment: The word "minimum" in the second sentence below should be "maximum"
Perhaps some insight is given by the graph at the right. The fixed perimeter is
2a + 2b = 10.
The red graph represents the area function of the graph as either of a or b varies from 0 to 5. Let b represent the length of one side and 5 - b the length of the other.
Area = ab = b(5 - b) for 0 < b < 5
When the AM-GM Inequality is applied we get Area ≤
Points on the blue curve, Area = 6.25 are always greater than points on the red curve (That is, the area of the rectangle is always less that 6.25) and the blue curve (a horizontal line representing a constant) is tangent to the red curve if and only if b = (5 - b), i.e., b =2.5.
Setting this up with the usual function notation, let the Perimeter of the rectangle equal 10 and let one side be x. The the other side is 5 - x.
The utility of the AM-GM Inequality is that the replacement function after the application of the AM-GM inequality is a constant line tangent to the previous function. The area is always less than the constant AND it is equal to that constant when a = b. In our example for P = 10, a = b = 2.5 when the rectangle is a square.
From my web page, here is a problem posed for students:
The second problem, where ab is a constant rather than a + b, is a nice contrast to the first and it also follows quickly from the AM-GM Inequality:
Alternative Proofs and Demonstrations
of the
Arithmetic Mean-Geometric Mean Inequality
In this section, I will limit the exploration to the simplest case: The arithmetic mean and geometric mean of two positive numbers. In my Problem Solving course I pose AS AN EXPLORATION that the student find a least 5 demonstrations or proofs. Seeing multiple approaches to this relation can help with understanding it, seeing its importance, and finding it useful as a problem solving tool.
Some algebra
A Geometric Demonstration
Another Geometric Suggestion
Construct a semicircle with a diameter a + b. The radius will be the Arithmetic Mean of a and b. Construct a perpendicular to the diameter from common endpoint of the segments of length a and b. From the intersection of this perpendicular with the semicircle construct the red segment. This segment will always have a length less than or equal to the radius of the circle and it will be equal only if a = b.
This example is closely related to the well known geometric theorem that the altitude of a right triangle from the 90 degree vertex to the hypothenuse will be the geometric mean of the two segments cut off on the hypotenuse.
Another Geometry Example
Another Algebra Demonstration
This demonstration begins with the identity:
Since
we have
with equality if and only if a = b.
Given two tangent circles of radii a and b. Construct a common external tangent to the two circl3s and draw radii of each circle to the common tangent. Find the length indicatec by ? along the common tanget in terms of a and b.
Solution: by constructing a segment parallel to the one under study, a right triangle with legs of length ? and a-b, and hypotenuse of length a+b. the segment along the common tangent has length twice the geometric mean of a and b.
Consider a circle with chords AB and CD. Let the CD pass through the midpoint M of AB.
Let AM = MB = z and let CM = x, MD = y. The lengths are all positive values.
By an elementary theorem of geometry the products of the parts of the chords are equal.
We know that x + y ≥ 2z with equality only if M is the midpoint of CD.
Solving Problems with the AM-GM Inequality
Cost of Fencing a Field
Problem: A farmer wants to fence in 60,000 square feet of land in a rectangular plot along a straight highway. The fence he plans to use along the highway costs $2 per foot, while the fence for the other three sides costs $1 per foot. How much of each type of fence will he have to buy in order to keep expenses to a minimum? What is the minimum expense?
Solution: (This is a typical calculus problem but no calculus is needed!)
Minimum of
The problem is to find minimum values for this function in the range or 0 < x < π. This one requires some change in the form of the equation in order to apply the AM-GM Inequality. First, however, it is helpful to see a graph and have some sense of the equation. The graph at the right suggests that there may be two minimum values in the range 0 < x < π.
Construct a Square with Same Area as a Given Rectangle
The problem is to construct a square with straightedge and compass that is the same area as a given rectangle.
The area will be ab and so the length of the side of the square is the geometric mean.
Consider:
The red segment is the geometric mean of a and b.
Maximum Area of a Sector of a Circle With Fixed Perimeter
Understanding the problem. A sector of a circle has a perimeter made up of two radii and an arc of the circle connecting the endpoints of the two radii. Compare the areas of three sectors -- each with P = 100 -- central angles of 45 degrees, 90 degrees, and 180 degrees. These are sectors that are an eighth circle, quarter circle, and semicircle. As the angles increas, the radii become shorter because more of the fixed perimeter is in the arc. Note these angles are
When these three areas are computed we get
Clearly, as the angle increases from 45 to 90 to 180 the area increases and then decreases. Somewhere there is a maximum area. Where?
Sector as Fraction of a Circle
Some students (and teachers) have an aversion to working with radian measure. For them the approach might be as follows:
Let k be the fraction of a circle represented by the sector. 0 < k < 1. The Perimeter is a constant and so we can represent it as twice the radius plus the fraction of the circumference.
The area of the sector in the fraction notation can be formed as either a function of r or a function of k, depending on a subsitution of r or k from the perimeter equation. Either one can be used with the AM-GM Inequality to reach closure on the problem:
Looking back at the example when P = 100, the maximum area would be when r = 25 and therefore the arc length is 50. The angle is a little less than 120 degrees.
Sector in Radian Measure
The parallel of this solution with the one where the square was the maximum area for rectangles with fixed perimeter is worth noting.
Inequalities Problems
Comparison of altitude and median in a right triangle
Construct segments from the endpoints of the diameter to complete a right triangle.
Maximum and Minimum of
Rewrite
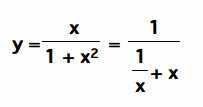
For x > 0, using the arithmetic mean-geometric mean inequality,
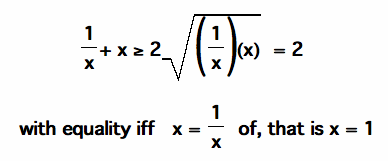
Therefore the value of the function is always less than or equal to .5 and it is equal to .5 only when x = 1.
For x < 0, a similar argument leads to finding the minimum of the function at x = -1. Since the Arithmetic Mean -- Geometric Mean Inequality holds only for postitive values, when x < 0 we have to apply the inequality to - x and - 1/x. We know
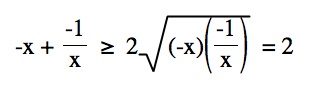
Keep in mind this is for x< 0 so -x and -1/x are postive. Multiplying each side of the inequality by -1 gives
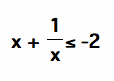
and equality occurs when x = -1. Therefore the value of the function is always more than or equal to -0.5 and it is equal to -0.5 only when x = -1.
Maximum of f(x) = (1-x)(1+x)(1+x)
We have three factors in the function and we want to know when the function reaches a maximum in the interval [0,1].
In order to take advantage of the AM-GM Inequality, we need the sum of these factors to equal a constant. That is we need -2x rather than -x. We can get that by the following
The function reaches this maximum value for x in [0,1] if and only if
2(1 - x) = 1 + x
2 - 2x = 1 + x
1 = 3xThat is,
Minimum Surface Area of a Can of Fixed Volume
In packaging a product in a can the shape of right circular cylinder, various factors such as tradition and supposed customer preferences may enter into decisions about what shape (e.g. short and fat vs. tall and skinny) can might be used for a fixed volume. Note, for example, all 12 oz. soda cans have the same shape -- a height of about 5 inches and a radius of about 1.25 inches. Why?
What if the decison was based on minimizing the material used to make the can? This would mean that for a fixed volume V the shape of the can (e.g. the radius and the height) would be determined by the minimum surface area for the can. What is the relationship between the radius and the height in order to minimize the surface area for a fixed volume?
What would be the shape of a 12 ounce soda can that minimizes the amount of aluminum in the can?The Volume is fixed.
The Surface area is a function of r and h.
What is the minimum S?
( Note that we have use the AM-GM Inequality for three positive numbers)
Maximum area of a Pen, fixed length of fencing, with Partitions Parallel to a Side
Suppose you have 100 feet of fencing. You want a rectangular pen with a partition parallel to a side. The 100 feet of fencing must enclose the four sides and the partition. What is the shape of the pen and what is the maximum area?
Show that the dimensions of the maximum area pen is 25 ft. by 16.67 ft. with maxim area of approximately 417.7 sq. ft.
Prove the Maximum Area of a Triangle with Fixed Perimeter is Equilateral
Minimum Distance from (0,0) to
Find a point on the graph of
that is closest to the origin.
(follow the link to the discussion)
Maximum Area of a Triangle with Sides of 9, 40x, and 41x
Given a triangle with one side of length 9 units and the ratio of the other two sides is 40/41.
Find the Maximum Area.
(use link for discussion)
The Box Problem
Use the Arithmetic Mean-Geometric Mean Inequality to find the maximum volume of a box made from a 25 by 25 square sheet of cardboard by removing a small square from each corner and folding up the sides to form a lidless box.
Theorem: In the Product of n positive numbers is equal to 1 then the sum if the numbers is greater than or equal to n.
Clearly, the proof of 3 implies the first two.
This sets up an efficient process for obtaining successive estimates with a hand calculator, a spreadsheet, or by paper and pencil. On the right is a part of a sqreadsheet showing calculation for
. The process quickly converges to a good estimate.
Click HERE for the Excel file. Enter in cell A1 the value N for which the square root is wanted.