

Astroid Equations
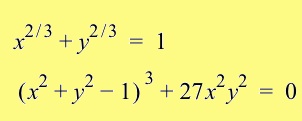
Show that the two equations at the right produce the same graph.
Click HERE for a GC 4.0 graph. Or HERE.
Here are Graphing Calculator graphs of the two equations:
The graphs look the same but some algebra is needed to show they are equivalent. Which would be easier:
a. Begin with the first equation and create the second? Need help? Click HERE.
b. Begin with the second equation and create the first?
c. Try either.
Build a GSP sketch to simulate a small circle of radius r rolling around the inside of a larger circle of radius R, where R = 4r. Trace the locus of a point on the rim of the small circle as it rolls around the inside of the larger circle.
Click HERE for a JavaGSP demonstration. If Java does not work, click HERE for GSP animation.
An astroid can also be generated by an envelope of line segments where one end of the segment is moved along the x-axis and the other is moved along the y-axis. To the right is an astroid produced by a GSP implementation.
Click HERE to open the GSP file and see the astroid generated. Use erase changes to refresh the figure.
Intesting variations can be found. Try for each with your own GSP.
a. Try a GSP file with non-perpendicular axes.
b. Trace the midpoint of the line segments.
c. Trace a non-midpoint on the line segments.
d. Create a figure where the line segments change length.
a.
b.
c.
d.