
Bisector of An Angle of a triangle.

Exploration
Construct any triangle. Construct an angle bisector in the triangle and draw the segment along the angle bisector from the vertex to the intersection with the opposite side.

Click here for a GSP Sketch to explore these ratios.
TO PROVE
The bisector of an angle of a triangle divides the opposite side into segments that are proportional to the adjacent sides.
That is, for any triangle ABC, the bisector of the angle at C divides the opposite side into segments of length x and y such that
Hint 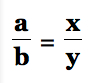
Extension
Prove that the bisector of an exterior angle of a triangle divides the opposite side externally into segments that are proportional to the adjacent sides.
That is, the external bisector of the angle at C externally divides the side AB at M such that
Hint: Draw AE parallel to CD.
Extension
Given a set of triangles all having the same base AB. What is the locus of the vertex C in the ratio of the sides adjacent to C is 1? Proof?
Extension
Given a set of triangles all having the same base AB. What is the locus of the vertex C in the ratio of the sides adjacent to C is not equal to 1? Proof?
Build a GSP sketch to draw this locus. Click here to see a GSP animation.
Return to the EMAT 6600 Page