A circular disc of radius R is used to make a right circular cone by removing a sector with angle
and then joining the edges where the sector was removed. What is the maximum volume that such a cone can attain? That is, what angle
Suggestion: Make a physical model to demonstrate to yourself or to others how a cone is formed from a circular disc in this way. Cutting a circular disk out of the stock of a manila folder is about the right weight. Rather than completely removing the sector you are taking out, try cutting along a single radius. Then slide the edges over the top of one another to form a cone.
In this illustration the sector of the circular disc is removed and the edges joined to form the cone as shown below where r is the radius of the base of the cone. The circumference of the base of the cone is r =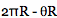
This is a standard calculus problem. Can you find ways to investigate the problem without calculus?
Suggestion:
Determine a function for the volume as the angle is varied. Make a graph of the function. Interpret the graph.Suggestion:
Try building a model of the problem with GSP.Suggestion:
Try building a spreadsheet with the volume determined for different angles.Suggestion:
Try using the AM-GM inequality. Why does it NOT work?
Do you need Help with setting up the algebra for this?