

Suppose you are given a triangle with sides of lengths a, b, and c. Let the semiperimeter be defined by
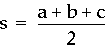
.
If s(s - c) = (s - a)(s - b), what can you conclude about the triangle?
Hints/Solution:
Expand each side of the equation . . . Do you have a proof that the triangle must be a right triangle?
Did you use the Pythagoran Theorem? Or, did you use its converse?
Comments:
Is there a geometric interpretation of s(s-c) or (s-a)(s-b)? Let's construct the incircle for triangle ABC and label the respective distances from A, B, and C to the points of tangency as x, y, and z respectively:
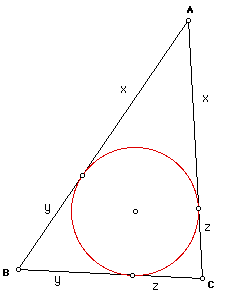
Now it is relative easy to see that
a = y + z
b = x + z
c = x + y
s = x + y + z
x = s - a
y = s - b
z = s - c
By constructing lines parallel to AC and BC we see a figure that is twice the area of triangle ABC.
Extensions/Variations:
Converse. If your conclusion was given, could you conclude that s(s - c) = (s - a)(s - b) ? That is, if the triangle is a right triangle, prove that this equation must hold.
Cyclic Quadrilateral Extension. Construct a segment of length equal to the semiperimeter from the point of tangency D on AB along the perpendicular to AB. Show that AHBI is a cyclic quadrilateral if and only if angle C is a right angle. Go to Cyclic Quadrilateral Extension.
Reference:
Coxeter, H. S. M., (1989). Introduction to Geometry (2nd ed.). New York: Wiley.