

Projections: Homothetic Similarity
Given a point P and two figures positioned in such a way that a ray from P to a point on the first figure contains the corresponding point on the second figure and visa versa. Further if X and X' are corresponding points, the distances from P to any point X and to distance from P to X' is proportional for all corresponding points. Let k be the proportionality constant (also called a coefficient of similarity). That is, PX = kPX' for all X.
Examples: 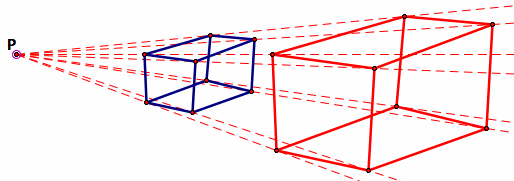
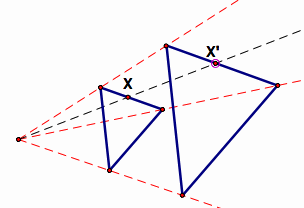
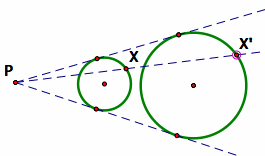
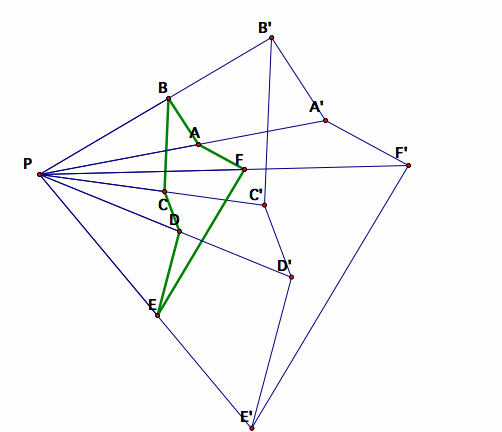
Four Problems:
PROVE: Given the above conditions, if X and Y are points in the first figure then the corresponding points in the second figure X' and Y' will have X'Y' = kXY and XY will be parallel to X'Y'.
PROVE: The figures will be similar.
PROVE: For all X, PX = kXX'
PROVE: All circles with common external tangents from a point P will be similar with radius of the second circle will be kr, r the radius of the first circle.