

Suppose two right triangles, each with hypotenuse of length 1, are placed
as in the following figure. The acute angle with measure A in the first
triangle (yellow) is placed at the acute vertex opposite acute angle B in
the second triangle (blue). Since the hypotenuse is of length 1 in each
case we have a physical representations of sin A, sin B, cos A, and cos
B as indicated in the figure.
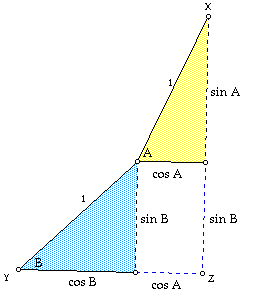
By drawing segment XY we can complete a right triangle with legs of
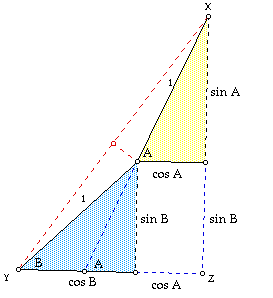
Determine the length of XY in terms of the cosine and sine of some angle
and then write trigonometric identities for sin A + sin B and for cos A
+ cos B.
Hint: Pay attention to the dotted line in the blue triangle that intersects
the leg of the right triangle at an angle of measure A.