

A frustum may be formed from a right circular cone by cutting off the tip of the cone with a cut perpendicular to the height, forming a lower base and an upper base that are circular and parallel. The problem can be generalized to other cones and n-sided pyramids but for the moment consider the right circular cone.
Let h be the height, R the radius of the lower base, and r the radius of the upper base. One picture of the frustum is the following.
Given R, r, and h, find the volume of the frustum.
Hint: (Consider the difference of two cones)
The Formula
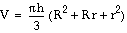
Problems:
1. Derive the formula. Calculus is not needed, although many calculus-based derivations can be found on Google.
1a. Grumpy Throckmorton writes:
Amazing how closely the frustum of a right circular cone resembles a beer glass, isn't it?! ;)
I got curious about the volume of just such a glass the other day and set off to find the answer with no tools other than a pen and a paper napkin.
You present a nice compact formula: ... but it's in terms of "h".
In practical terms, "h" is kinda hard to measure. A more interesting problem - one that took me through a delightful review of algebra and trigonometry - is to express it in terms of "s", the length of the side (a much easier measurement to make).
Can you write a compact expression for the solution in terms of "s"?
Express the volume in terms of R, r, and s.
2. What is the area of the curved surface of the frustum of a right circular cone? What is the total surface area of the frustum?
3. What is the volume of a frustum formed from square based pyramid of height h, lower base having a side length of S, and an upper base of side length s?
Note: See Polya, G. (1965) Mathematical Discovery: On Understanding, Learning, and Teaching Problem Solving, Volume II, Chapter 7, pp. 1-21, for discussions of finding the volume of a square based frustum.
4. What is the total surface area of the square based frustum?
Return to EMAT 4600/6600 Page.