

This problem investigates one connection between the Golden Ratio and the Fibonacci Sequence.
The Fibonacci Sequence 1, 1, 2, 3, 5, 8, 13, 21, . . . begins with F(1) = 1, F(2) = 1 and nth term, n > 2 is denoted by
F(n) = F(n-1) + F(n-2).
Create a Spreadsheet to generate the Fibonacci Sequence. (or, Click HERE)
See the Sublime Triangle for one derivation of the Golden Ratio. In the sublime triangle, the sides are of length a + b and we have the ratio
. This is the Definition of the Golden Ratio -- a segment divided into two parts such that the ratio of the total to the longest part is the same as the ration of the longest part to the shortest part.
by setting
the equations
can be used to find
. Now, use the first equation to generate a sequence of positive powers of the Golden Ratio:
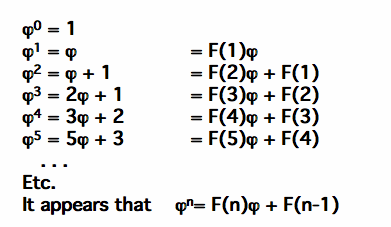
Verify each of these by pursuing the relevant algebra, e.g.
PROVE with Mathematical Induction:
Need help finishing the proof?
Find the sequence of powers of
for NEGAGIVE integers.
Begin with
Continue and create a general expression to prove by mathematical induction.