

Jordan's inequality states that for
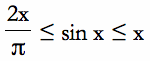
Prove Jordan's Inequality.
Discussion:
What does this inequality say? We have a curve, y = sin x, placed between two linear functions in the range
. The inequality is reversed in the range
. One interpretation of this is that in this range, the value of sin x is always less than the curve tangent to the sine curce at the origin (y = x) and it always lies above the chord of the sine curve between the origin and
.
So what? Why is the Jordan Inequality important in pure or applied mathematics?
Who was Jordan?
HINTS for thinking about a proof:
Consider a unit circle, OA = 1 with a point P on the circle. Construct a perpendicular from P to the x-axis with M being the foot of the perpendicular and Q its reflection in the x-axis. Let x be the measure of the angle POM. The line PM has length sin x.
Construct a circle of radius MP and center at M.
Find elements in the figure that reflect what you are to prove in Jordan's Inequality.
Reference: Yuefeng, Feng. (1996) Proof without words. Mathematics Magazine. 69, p. 126.