

Area of a Lune
A lune is a plane figure bounded by the arcs of two circles. As a planar figure, the lune has an area but determining the area may be a challenge.
It is well known that a square with the same area as a circle can not be constructed with straightedge and compass. Surprisingly, even though the lune is bounded by arcs of circles, some lunar shapes can be shown to have a constructable square of the same area.
Given a right triangle ABC. Construct a lune with vertices at A and C with the center of the inner arc being at C and the center of the outer arc being at the midpoint of segment AB.
Prove that the area of the lune so constructed is the same as the area of the triangle ABC.
Some auxillary figures that may be helpful. For example, either of the following could be useful:
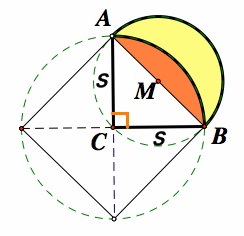
Hints: (If you want or need them).
This is sometimes described as a "lune formed on the side of a square" and is associated with Hippocrates, who discovered a construction that showed a square with the same areas as this lune could be constructed using straightedge and compass.
It is, of course, a special Lune. There are exactly 5 lunes for which a construction can be found to create a square of the same area using straightedge and compass. The proof that there are exactly 5 is quite challenging and the construction of the other 4 is also much more involved than this one. Usually, trigonometric analyses are used to prove there are exactly 5.
Click HERE for a link to an excellent paper on the Five Squarable Lunes.