

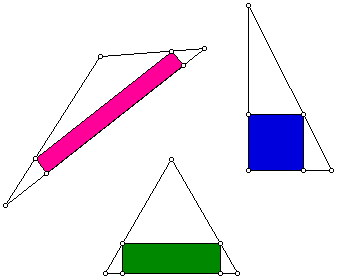
Consider the four vertices of a rectangle. To have a rectangle inscribed in a triangle, two of the rectangle's vertices must lie on the same side of the triangle. Here are some examples at the right.
Given a triangle, construct the inscribed rectangle with maximum area. Is there a "maximum" rectangle for each side of the triangle?
What is the relation of the area of the rectangle to the area of the original triangle? Prove it!
Hint -- a drawing and some notation.
Further hint (only if desparately needed): Click Here