

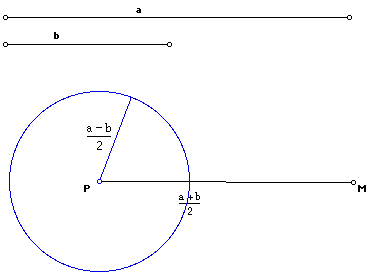
Consider two segments of lengths a and b. Construct two new segments, one half the difference in these two lengths and one half the sum. Use half the difference as the radius of a circle at P. Construct PM as the half sum. Clearly PM represents the arithmetic mean of a and b.
Construct a tangent from the circle from M to obtain the segment MN.
Construct a perpendicular from P to the circle at R and construct RM.
Construct perpendicular from N to PM. Label the intersection S.
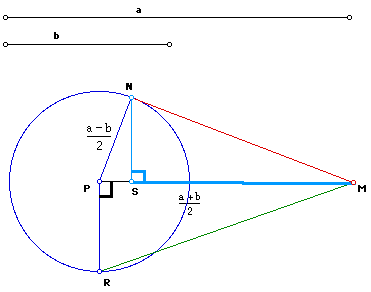
Find MN in terms of a and b.
Find MR in terms of a and b.
Find MS in terms of a and b.
Discussion:
From the construction it is clear that when a > b,
MS < MN < MP < MR
and they would be equal if a = b. Interpret.
Click here for a JAVA GSP animation. Use the Back Key to return.
Click here to download a GSP animation.