Triangles and Squares
At least Three Different Problems
Consider any triangle ABC. Construct a square to the outside
of the triangle on each side.
Generate a GSP construction to explore this configuration.
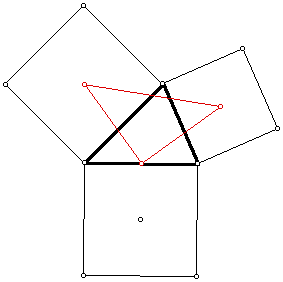
Select any two square centers and the midpoint of the other side
of triangle ABC. Explore the triangle formed by these three points.
Conjecture?
Proof?
Explore the relationship of two segments, one being
defined by a vertex of the triangle and the center of the square
on the opposite side and the other being defined by the centers
of the squares on the sides adjacent to the vertex.
Conjecture?
Proof?
Note that there are three pairs of such segments.
Explore the same relationships when the square
on each side is constructed toward the interior of the triangle
Prove that the three lines from the vertices to the centers
of the squares on the opposite sides are concurrent.
Return to the EMAT
4600/6600 Page