Locus of a Point in a Triangle
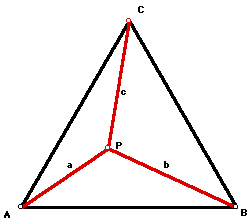
Given an equilateral triangle ABC with sides of length 1. Let
P be a point in the plane of ABC and let a, b, and c be the respective
distances PA, PB, and PC. What is the locus of P for a+b+c = K,
where K is a constant greater than 
?
For any triangle, the minimum sum of the distances from an
interior point to the three vertices is when the interior point
is the Fermat point -- the point where each of the sides of the
triangle is under an angle of 120 degrees. Therefore, when K is
in
the present case of the unit equilateral triangle, the locus is
a single point.
When K = 2, each of the vertices is part of the locus, and further, no point on the interior of the triangle is part of the locus.
An attempt that did not go anywhere -- yet.
A Geometrer's SketchPad drawing produced the following estimates of points on the locus when the length of a+b+c was about 1.9. This was done by dividing a fixed line segment into three parts and then constructing circles from each of the three vertices. The parts of the fixed segment could be varied to find common intersection points. Not satisfactory, but convinicing that the locus is not a circle.
Is this locus constructable with elementary geometry tools?
First, choose a position in the coordinate system and locate the three vertices A, B, and C
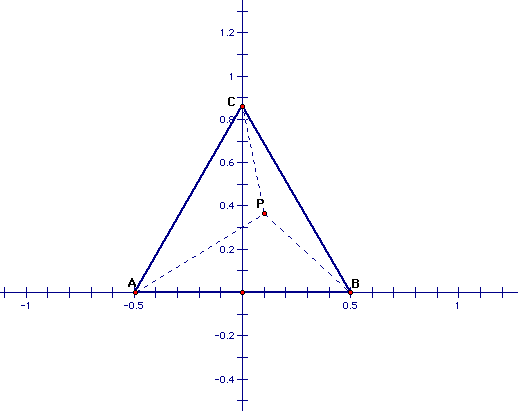
Using the distance function, write a formula for the distances PA, PB, and PC where (x,y) is the variable point P.
Here are the graphs for K = 1.8, 2, and 2.2. Click here for a Graphing Calculator file. Vary K.
The following peicture shows the graphs of the locus, from inside to outside, for various values of K.
And, in living color, without the superimposed drawing of the triangle:
Consider the acute scalene triangle with vertices at A = (-1, 0), B = (3, 0), and C = (0,2). The loci for values of K from about 5.5 to 7.7 are shown below.
The triangle ABC has not been superimposed on this picture.
