

Find at least 5 different ways to develop a closed form formula for the sum of the first n natural numbers.
Which lead to understanding of the formula?
Which lead to proof of the formula?
T(n) = 1 + 2 + 3 + 4 + . . . + n
T(n) is the nth Triangular Number. Perhaps they are so named because they can be represented by a triangular array of dots:
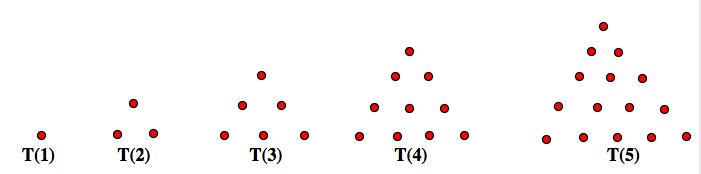
or by a triangular array of blocks:
Using blocks to construct representations of triangular numbers can be adapted to using classroom cubes to show these patterns. Or they can be nicely constructed using grid paper.
Hints:
Try to find approaches that are
Numerical
1. Look for a pattern. For example:
This is an iterative form for generating triangular numbers; we want to find a closed form.
2. For example, write the sum "forward" and "backward". Then add the respective sides of the two equations
3. Implement a spreadsheet to write a column of trianglar numbers
Click HERE for an Excel file that shows a graph for the first 40 triangular numbers.
Geometric
1. Use the dot patterns above. Take any two adjacent triangle numbers and combine the two triangular arrays into a square array.
2. Use the block pattern for this same strategy.
3. Use the dot patterns above. Take ONE tranglular number and double it.
4. Use the block pattern with this same strategy.
Use the Arithmetic Mean
T(n) = 1 + 2 + 3 + . . . + n-2 + n-1 + n
Arithmetic Series
1 + 2 + 3 + 4 + . . . + n is an arithmetic series if n terms with initial term 1 and common difference d = 1.
Algebraic
1.
This approach was presented by Polya in Mathematical Discovery. It has the additional value in that it provide a technique that can be generalized easily for explore closed formulas for the sum of the first n integer squares, the first n integer cubes, etc.
2.
See Sums of Powers of Integers -- Derivations from Summations for more discussion and extension of this strategy to finding the closed form for sums of powers of integers.
Mathematical Induction
Mathematical induction provides one means for proof of the closed form formula. It does not provide a means to derive the formula, but rather to confirm via proof.
Use mathematical induction to prove the formula for T(n).
Finite Difference Methods
See Using the Technique of Finite Differences: Examples and Problems
The case for T(n) is one of the examples.