

Triangular Number Problems
1. Prove that for any consecutive triangular numbers T(n-1) and T(n),
2. Note the sequence of trianglar numbers begins 1, 3, 6, 10, 15, . . .
Write the beginning numbers for the sequence of SUMS of trianglular numbers.
Find an closed form expression for the sum of the trianglular numbers,
T(1) + T(2) + T(3) + . . . + T(n).
3. Handshake problem.
An at meeting on 18 members of a club, each member shakes hands with every other member exactly once. What is the total number of handshakes?
How many handshakes if there are 25 members in attendance?
How many handshakes for n members?
4. When distinct 9 points are placed on a circle, how many segments are determined? (do not consider the intersections of the segments within the circle to determin new points and segments).
What if there are n points?
Segments connecting adjacent points are the sides of a convex polygon. Segments connecting non-adjacent points are diagonals.
Write a formula for the number diagonals of an n-sided convex polygon.
5. If we have n objects in a set selected 2 at a time, what is the number of combinations of n objects taken 2 at a time?
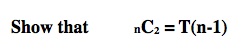
That is, show that the number of combinations of n objects taken 2 at a time is the (n - 1)st triangular number. That is, 1 + 2 + 3 + . . . + (n - 1).
6. Examine the Pascal Triangle for a line of triangular numbers. Explain.
Note: Each number in the Pascal triangle is the sum of the two numbers immediately above it. Numbers at the end of a row are seen to have a 0 and 1 immediately above them.
7. Find a line in the Pascal Triangle showing the sequence of SUMS of triangular numbers. Explain.
8. Find an expression for the first 2n integers.
1 + 2 + 3 + . . . + n + (n + 1) + (n + 2) + . . . + (2n - 1) + 2n = ?
9. Find an expression for the first n even integers: 2 + 4 + 6 + 8 + . . . + 2n
10. Find an expression for the first n ODD integers: 1 + 3 + 5 + 7 + . . . + (2n - 1).
Find five ways to show the sum of the first n odd integers.
For example:
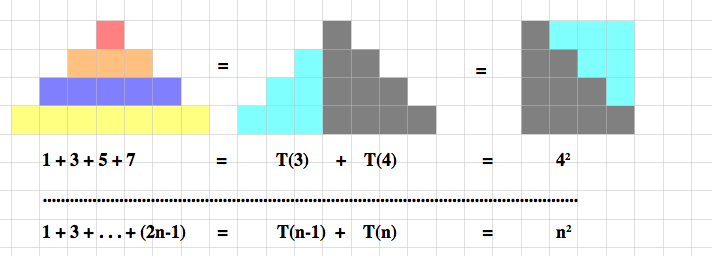
For example:
Show the sum of first n odd integers is
T(2n) - 2(T(n))
11. See Count the Triangles -- II
12. Find a reference for the "Rule of 78" -- a method that was used in lending to calculate yearly interst. Explain the "Rule of 78" in terms of triangular numbers.