
Right Triangle Inscribed in a Rectangle
with One Leg of Fixed Length
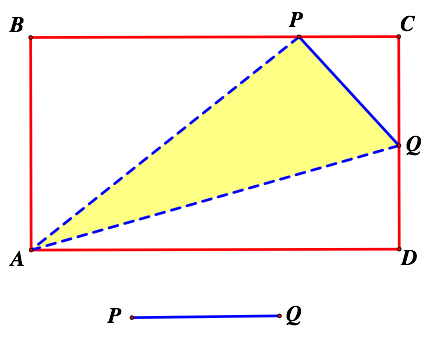
Given a rectangle ABCD of fixed dimensions a by b, and a line segment PQ of a fixed length, inscribe a triangle in the rectangle such that one vertex of the triangle is at Point A and P and Q are located on the sides opposite to A such that the triangle APQ is a RIGHT triangle.
First issue:
Show that to have triangle APQ to be a right triangle, triangles ABP and PCQ must be similar.
What problems do you encounter when you try for a straightedge and compass (or GSP) construction?
Show that the construction can not be accomplished with straightedge and compass.
An approach:
Introduce an x-y coordinate system with the rectangle located so that point A is at the origin. Label the figure as at the right.
Let x = BP and y = DQ. Our goal is to develop some equations expressing relationships between x and y. If we can find two such independent equations then the common solution will allow location of points P and Q .
All four triangles are right triangles and the given conditions of a, b, and s will allow use of the Pythagorean theorem to express the lengths of the internal lines.
This equation is the equation of a parabola that passes through points (0,b) and (a,b) and has axis of symmetry at x = ½ b.
Now, the given condition for the length of PQ is the hypotenuse of Triangle PCQ. Therefore we have:
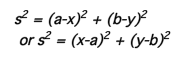
This is the equation for a circle of radius s with a center at (a,b). So considering together
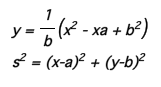
we have an image like that at the right. The result when a = 12, b = 10, and s =5 is shown. The intersection of the two curves is at (8.118, 6.849) and AP = 12.881 approximately.
The fact that the center of the circle is at (a,b) means one of the intersections will be at a point (m,n) such that m > a and n > b. Thus it is outside of the rectangle.