

Given two intersecting circles of the same radius with centers at D and E. Label the intersection points of the two circles A and F. Construct a circle with center at F with a radius so that this circle intersects both of the original circles. In points B and C and points G and H .
Show that A, B, and C are collinear. Show that A, G, and H are collinear.
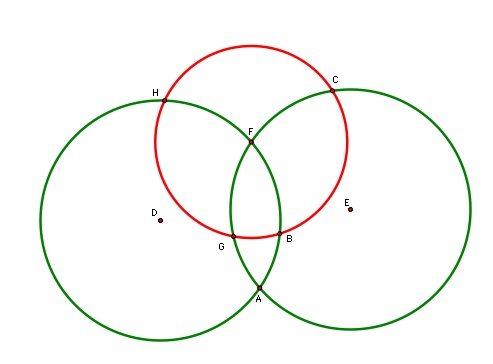
Make sure that your proof is still valid for the case when the radius of the circle centered at F is greater than FA by still allows the four intersection points.