

Problem: Develop a proof for Brahmagupta's Formula.
Who was Brahmagupta?
Brahmagupta's formula provides the area A of a cyclic quadrilateral (i.e., a simple quadrilateral that is inscribed in a circle) with sides of length a, b, c, and d as
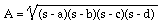
where s is the semiperimeter
Note: There are alternative approaches to this proof. The one outlined below is intuitive and elementary, but becomes tedious. A more elegant approach is available using trigonometry.
The use of Ptolemy's theorem (the product of the diagonals equals the sum of the products of opposite sides) may provide a different investigation of the problem.
If ABCD is a rectangle the formula is clear.
Consider the chord AC.
The angle that subtends a chord has measure that is half the measure of the intercepted arc. But the chord AC is simultaneously subtended by the angle at B and by the angle at D. There for the sum of these angles is 180 degrees. Opposite angles of a cyclic quadrilateral are supplemental.
Assume the quadrilateral is not a rectangle. WNLOG, extend AB and CD until they meet at P.
Label the extensions outside the circle e and f.
Now, triangles PBC and PDA are similar. Further, the ratio of similarity is d/b. Therefore the ratio of similarity of their areas is the square of this ratio, or,
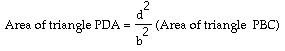
Now the area of the quadrilateral ABCD is the area of the larger triangle PBC less the area of the smaller triangle PDA. If A is the area of the quadrilateral and T is the area of triangle PBC
or
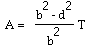
Now,
1. Heron's formula can be used to express the area of triangle PBC
2. The similarity of triangles PBC and PAD can be use to effect various (but tedious) substitutions.With appropriate perseverance and and algebraic subsitiutions/simplifications, Brahmagupta's theorem can be derived. To see a complete solution, click here.
Extensions:
1. If ABCD is a quadrilateral with sides of length a, b, c, and d, such that ABCD is both cyclic and has a circle inscribed in it, then use Brahmagupta's formula to show that the area of the quadrilateral is
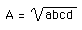
2. Consider Brahmagupta's formula as one side, say the one of length d wnlog, varies and approaches zero in length.
3. Use Brahmagupta's formula to develop equations for the length of the two diagonals of the quadrilateral.
References Bass, D. T., & Easterday, K. E. (1993). Using the Computer to Assess Inaccuracies in the History of Mathematics, The Mathematics Educator, 4, 54-59. (A proof of Brahmagupta's Theorem is in an Appendix to this article.)
Searcy, M. B. (1993). An exploration of Brahmagupta's Formula using The Geometer's Sketchpad, The Mathematics Educator, 4, 59-60.
Eves, H. (1990). An Introduction to the History of Mathematics (6th Edition). Philadelphia: Saunders, p. 227.
Hobson, E. W. (1904). A Treatise on Plane Trigonometry (4th Edition). New York: Macmillan, p. 204.
Johnson, R. A. (1929). Modern Geometry. Boston: Houghton-Mifflin, p. 81.