
6690 - Using Computers in Mathematics Instruction
Danie Brink
Essay 3 Linear Programming Continued
Step 4: Moving the objective function across the feasable region to intersect the feasable region at the optimum location in order to optimize the process.
In this example, the optimum point must be as high as possible on the feasable region since we are dealing with profit. If the objective function was a cost equation, we will attempt to intersect the feasable region as low as possible.
This is the location of the objective function
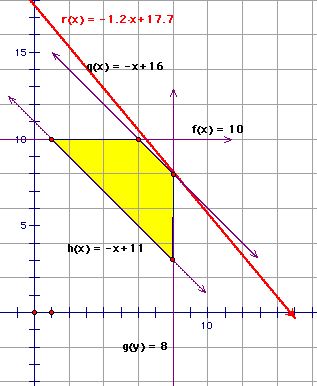
Now we can optimize the production of rugby balls. It happens where the objective funtion intersects the feasable region. We can clearly see that we will optimize our profit if we produce 8 type B rugby balls. To obtain the number of type A rugby balls, we substitute x = 8 into q(x) and see that we must produce 8 type A rugby ball. To see an animation of the objective function moving across the feasable region, click here.
Link to the Main Linear Programming Page
Link to the previous Linear Programming Page
Link to my 6680 Main Page
Link to my 6690 Main Page