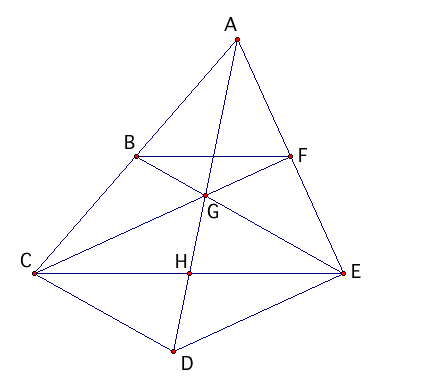
Given: In the figure alongside, B and F are the midpoints of sides AC and AE. AG = GD. R.T.P.: H is the center of CE, therefore AH is the third median of triangle ACE, therefore the medians of a triangle are concurrent. Proof: In triangle ACD, B and G are the midpoints of sides AC and AD. Therefore, BG//CD and BG = half the length of CD. In the same way it can be proven that FG//DE and FG = half of the length of DE. Since CG//DE and CD//GE, CDEG is a parallelogram. This makes CH=HE since the diagonals of a parallelogram bisect each other. Therefore AH is the third median of the triangle ACE. Therefore G, the point of intersection of the three medians is the point of concurrency. Q.E.D.

Back to Concurrency Page

Back to Main Page