Some useful definitions:

A median of a triangle is the line segment that joins a vertex of a triangle with the center of the opposite side.

An altitude of a triangle is the shortest distance from a vertex of the triangle to the opposite side. The altitude will intersect with the side perpendicularly and might be on the side or on an extention of the side.

A perpendicular bisector is a line segment that bisects the side of a triangle perpendicularly. This line segment is not the same as the height of a triangle since it does not necessarily go through the opposite vertex.

An angle bisector is the line segment that bisects any angle of a triangle.

Concurrent means "meet at a single same point" or "share a common point of intersection".

The medians of a triangle are concurrent. The medians intersect each other in a length ratio of 2 : 1. This point is called the centroid of the triangle.
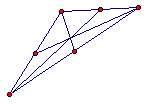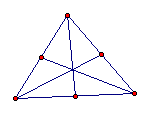The altitudes of a triangle are concurrent. The point of concurrency is called the orthocenter.
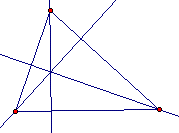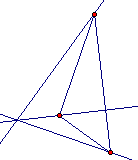The perpendicular bisectors of a triangle are concurrent. The point of concurrency is called the circumcenter.
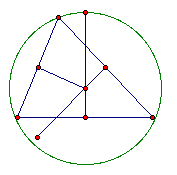The angle bisectors are concurrent. The point of concurrency is also the center of the incircle.

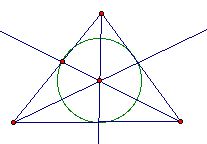Because the topic of concurrency is such an interesting, but big topic, I am going to make links to some of the topics here. That way, you can choose the topic that is of interest to you.

The interesting relationship between the orthocenter, circumcentre and centroid called Euler's Line.

The nine-point circle and how to construct it.

The proof of the theorem which states "The medians of a triangle are concurrent"

Back to Main Page