Assignment 9 continued: 

Pedal Triangles Part 3

by Kristina Dunbar, UGA

This page contains pedal triangles for special cases when the pedal point is the orthocenter, circumcenter, or center of the nine-point circle for triangle ABC.

What happens when the pedal point P is the orthocenter of triangle ABC?

Here's what it looks like:

The vertices of the pedal triangle when P is the orthocenter of the original triangle ABC are actually the intersections of the altitudes with their corresponding sides.

Unlike the cases with the centroid & incenter, the pedal triangle does not have to be inside the original triangle when the pedal point P is the orthocenter.  This is evident with the obtuse case below. 

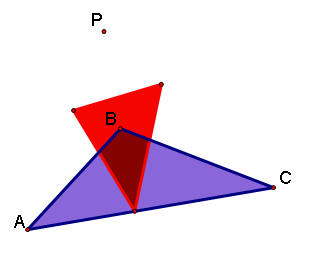
When the original triangle ABC is obtuse, the pedal triangle crosses the original triangle.   

When the pedal point is the orthocenter of the original triangle and the original triangle is a right triangle, the pedal triangle is actually the altitude of the triangle from the hypotenuse to the right angle.

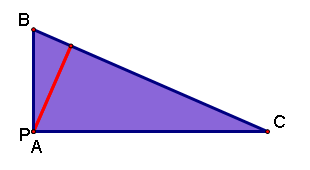
The above case is called the Simson line and is explored further in the next section on pedal triangles.  Click here to jump to that section of the next page.

Click here for a GSP construction of the pedal triangle when P is an orthocenter.

What happens when the pedal point P is the circumcenter of triangle ABC?

Here's what it looks like:

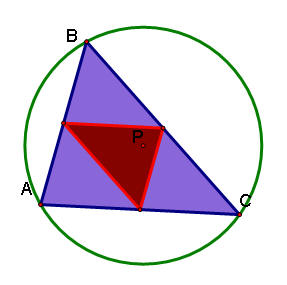
No matter what shape your original triangle is, the pedal triangle when the pedal point is the circumcenter is always inside the original triangle. 

Here are what the obtuse and right triangle cases look like:

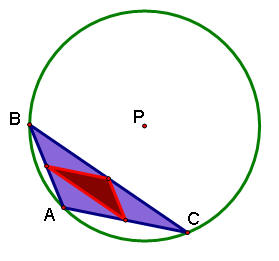
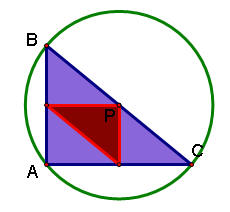
You see that in the case of the right triangle ABC above, the pedal point P is actually at the origin of the circumcircle.

Click here for a GSP construction of the pedal triangle when P is the circumcenter.

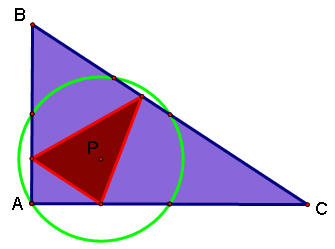
What happens when the pedal point P is the center of the nine-point circle of triangle ABC?

Here's what it looks like:

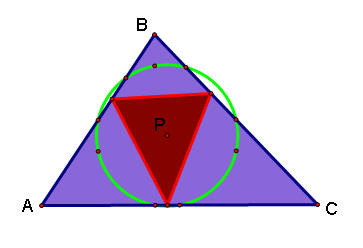
The pedal triangle does not have to be inside the original triangle.  In obtuse cases, it can be inside the original triangle or overlap it.  See the examples below:

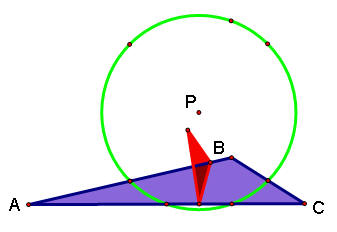
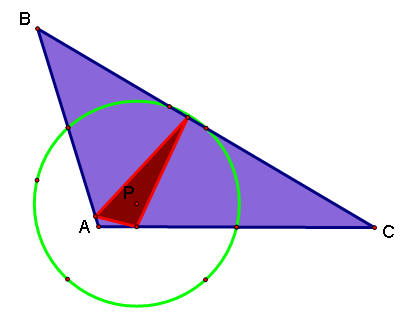
When the original triangle is a right triangle, the pedal triangle is inside the original triangle.

Click here for a GSP construction of the pedal triangle when P is the circumcenter.

Return to my Home Page.

Return to Pedal Triangles Page 1 or Page 2.

Return to TOP.

Continue Exploring Pedal Triangles.