Assignment 9 continued: 

Pedal Triangles & the Simson Line

by Kristina Dunbar, UGA

This page contains pedal triangles for special cases when the pedal point is on a side of the original triangle or at a vertex.  We also discuss Simson Lines.

What happens when the pedal point P is on a side of triangle ABC?

Here's what it looks like:

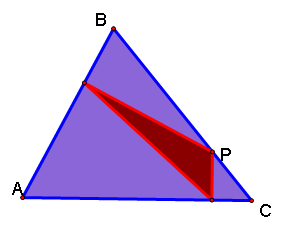
The above case is for an acute triangle.  When the triangle is obtuse, it looks like this:

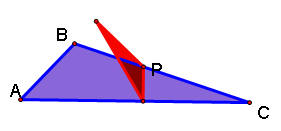
When the original triangle is right, the pedal triangle looks like the one below:

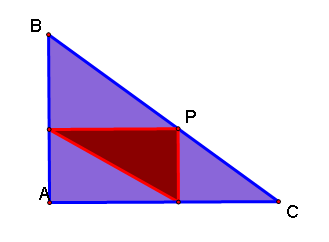
The pedal triangle is also a right angle!

Click here for a GSP construction of the above cases.

What happens when the pedal point P is on a vertex of triangle ABC?

Here's what it looks like:

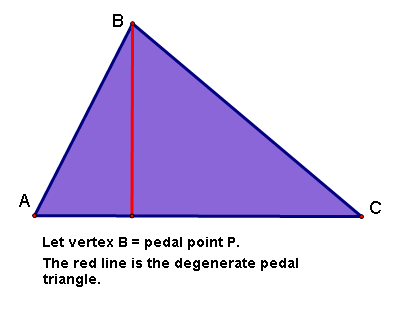
When the pedal point P is on a vertex of the original triangle, all of the vertices of the pedal triangle are collinear. 

A Simson Line is when all three vertices of the pedal triangle are collinear, forming a degenerate triangle.

When the pedal point is on a vertex of the original triangle, it does not matter what shape the original triangle is, the pedal triangle will always form the Simson Line.  In the case where P is on a vertex, the Simson Line will always be an altitude of the original triangle.  However, there are other cases in which the pedal triangle is a Simson Line, and it does not always have to be an altitude.

Return to my Home Page.

Return to Pedal Triangles Page 1, Page 2, or Page 3.

Return to TOP.

Continue Exploring Pedal Triangles.