Pedal Triangles Page 5

by Kristina Dunbar, UGA

We will only look at a few more cases of pedal triangles.

When the pedal point is on the circumcircle of a triangle ABC, the pedal triangle is the Simson Line.

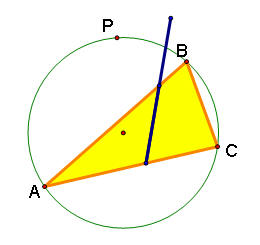
Click here for a GSP animation of the above construction.

The below picture shows the path (in pink) of the Simson Line as the pedal point moves around the circle.

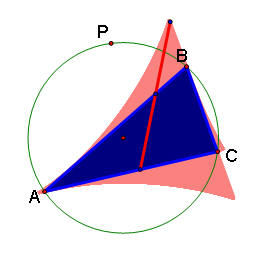
We can also have the pedal point P move around a circle with a larger radius than the circumcircle.  Here's what that will look like.

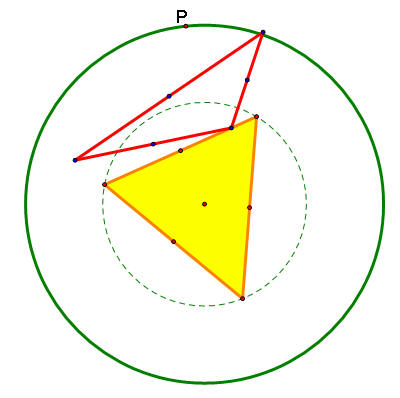
As P moves around this larger circle, let's look at the path of the midpoints of the sides of the pedal triangle.  We see that they form ellipses (in blue).

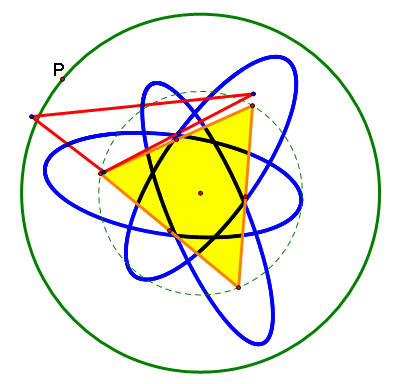
Click here for a GSP animation of this.

The following is a picture of what would happen if the pedal point P were on the circumcircle of the original triangle, forming a Simson Line.  In the below case, we extended the Simson Line to a longer parallel line instead of just a line segment.  The traces show what path this line takes as P moves around the circumcircle.

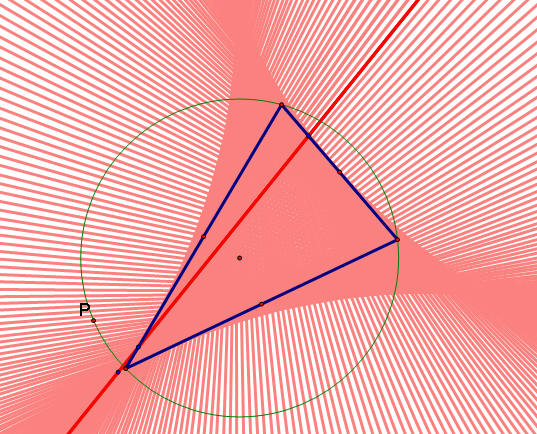
Return to my Home Page.

Return to Pedal Triangles Page 1, Page 2, Page 3, or Page 4.

Return to TOP.