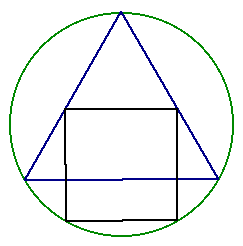
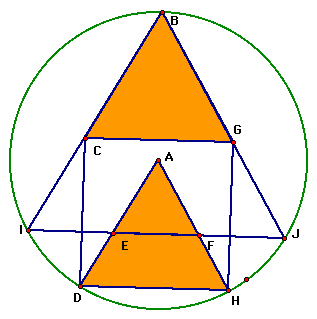
Now that we've discovered a construction of the inscribed problem (shown below) we should take some time to investigate its peculiar properties.

A foundation of this figure is the equilateral triangle that was initially constructed. Our completed construction hints that more equilaterals may be lurking in this figure than we initally thought. Investigate the figures in this Geometer's Sketchpad file and see if you can find more equilateral triangles.
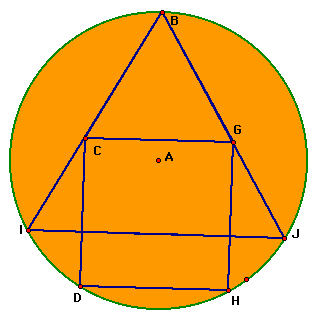
By drawing radii to the vertices of the square we find the following triangle which appears to be equilateral - check it out below.
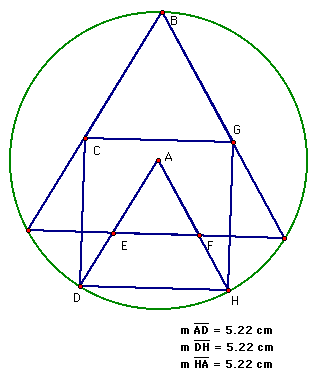
While measuring the sides of triangle ADH offers evidence that the triangle is equilateral, a more careful proof is needed to confirm this conjecture.
Let's begin the proof by looking back at the construction of point D. To find D, we constructed segment IJ' which was perpendicular and congruent to segment IJ. By connecting points B and J' and locating that segment's intersection with the circle one vertex of the square (point D) was located.


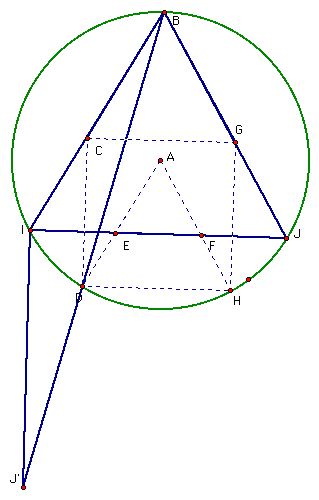
Since triangle BIJ is equilateral, the measure of angle BIJ is 60 degrees. Since segment IJ' is perpendicular to segment IJ, then the measure of angle J'IJ is 90 degrees. Consequently, the measure of angle J'IB is 150 degrees. By construction, segment J'I is congruent to segment JI and since triangle BIJ is equilateral, segment BI is congruent to segment IJ'. Thus triangle BIJ' is isosceles and it follows that the measure of angles IJ'B and IBJ' are congruent and have measure equal to 15 degrees.
By symmetry, we find that, in the figure below, angle JBI' also measures 15 degrees.
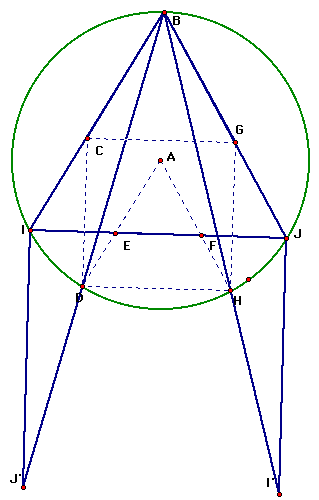
Since triangle BIJ is isosceles, the measure of angle IBJ is 60 degrees. Thus we find that the measure of angle DBH (and is 30 degrees). Consequently, the measure of minor arc DH is 60 degrees (twice the measure of its inscribed angle) and the measure of angle DAH equals 60 degrees.

Notice that segments AD and AH are both radii of the circle and necessarily congruent. Therefore triangle ADH is isosceles with vertex angle equal to 60 degrees. This means that angles ADH and AHD measure 60 degrees and ADH is equilateral.
Since segment DH is parallel to segment IJ, it necessarily follows that triangle AEF is also equilateral.
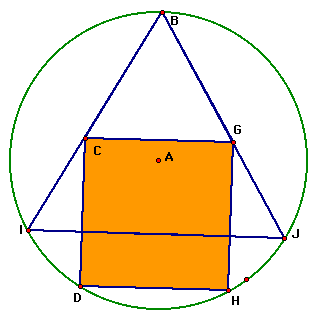
(1) Interestingly, triangle ADH being equilateral implies that the length of the side of our square must equal the radius of the circle. Examining ratios of area we find the following:
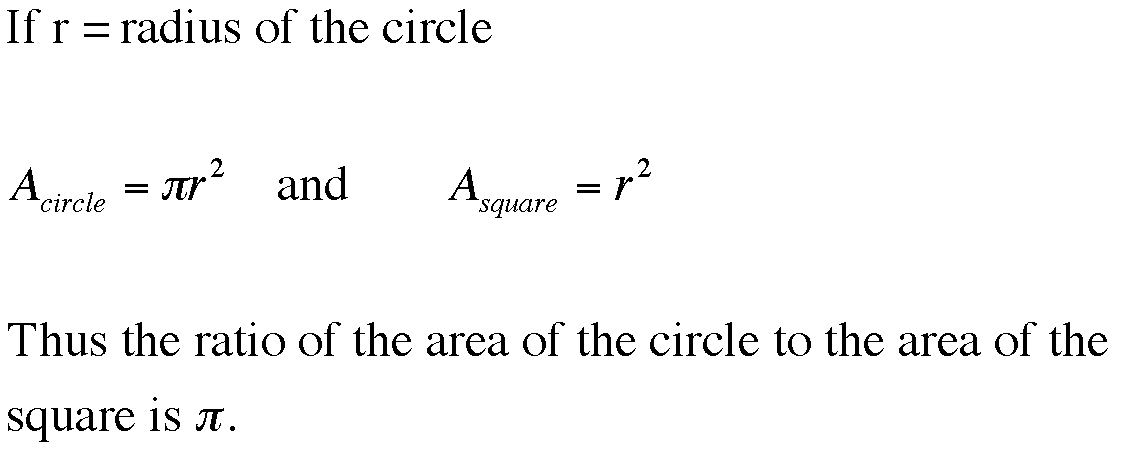
(2) Notice that the measure of angle AFE and BJI both equal 60 degrees. Examining segments AH and BJ cut by transversal JI, we see that angles AFE and BJI are corresponding angles. Since they are congruent we can conclude that segments AF and BJ are parallel. By symmetry we find that corresponding sides of triangles BIJ, AEF, and ADH are parallel.
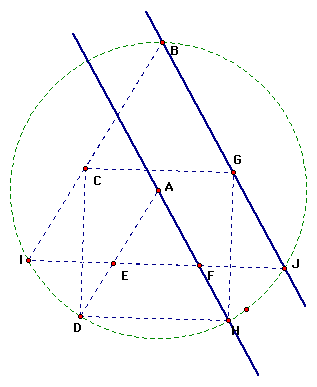
(3) Since CG is parallel to IJ, triangle BCG is also equilateral. It turns out that triangles BCG and DAH are congruent since they are both equilateral and contain a side of square CDHG.
(4) A circle can be partitioned into 12 congruent pieces by dividing the 360 degree central angle into 12, 30 degree angles. This results in the 12 equally spaced points seen below.
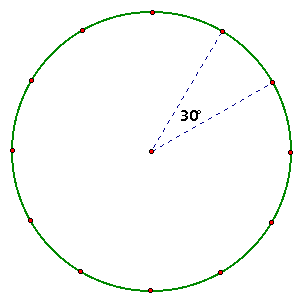
Since the measure of angle DAH is 60 degrees and the measure of angle IAJ is 120 degrees, we find that the vertices of the equilateral triangle and two vertices of the square lie on these points. This leads to an alternate construction of the desired figure.